CPU 和 MEM 也很重要！ · OSDI '22

去年我曾分析过一篇发表在 OSDI '21 上的论文 Pollux: Co-adaptive Cluster Scheduling for Goodput-Optimized Deep Learning。这篇论文针对深度学习任务提出了一种同时考虑作业层级（per-job level）信息和集群层级（cluster-wide level）信息的调度器，其实时地作出如下决策：

1. 调整每个作业的批处理数据大小和学习率；
2. 重新分配集群资源（GPU）。

具体内容请参见 面向深度学习的互适应调度 · OSDI '21。

本文将要讲述一篇发表在今年的 OSDI 上的论文 Looking Beyond GPUs for DNN Scheduling on Multi-Tenant Clusters。同样地，这篇论文也是一个针对 DNN 训练任务的调度 的工作。此文作者发现，尽管 GPU 是 DNN 训练所需要的最主要的资源，但是 CPU 和 MEM 的分配策略同样也会显著影响到集群的资源利用效率和训练任务的吞吐量。 由此，作者针对不同类型的 DNN，深入分析了 CPU 和 MEM 的不同组合对其吞吐量的影响，然后将最优的组合方案应用到了调度策略中。

接下来我将深入介绍这个工作。

1 研究动机

DNN 训练任务已经成为了云上的主要负载。面向这类任务的调度器，要么是通用的（如 Kubernetes、YARN），要么是针对其特性优化过的（如上文所述的 Pollux）。后者通常实现了一系列复杂的调度策略并针对 DNN 训练任务的平均完成时间（average job completion time，JCT）、全体完工时间（makespan）、或者其他指标进行了优化。现有的 DNN 调度器通常假设 GPU 是调度任务中占据主导地位的资源（dominant resources），只要 GPU 需求能够被满足，训练任务就可以被启动。而 CPU 或者 MEM 这样的资源，只需要按照 GPU 的占用比例进行分配即可（我们将其称为 GPU-proportional allocation），即：

$$ \begin{equation} \begin{aligned} \left\{ \begin{array}{l} \textrm{To-be-Allocated CPU} = \frac{\#\textrm{CPU}}{\#\textrm{GPU}} \times \textrm{Allocated GPU}, \\ \textrm{To-be-Allocated MEM} = \frac{\#\textrm{MEM}}{\#\textrm{GPU}} \times \textrm{Allocated GPU}. \end{array} \right. \end{aligned} \end{equation} $$

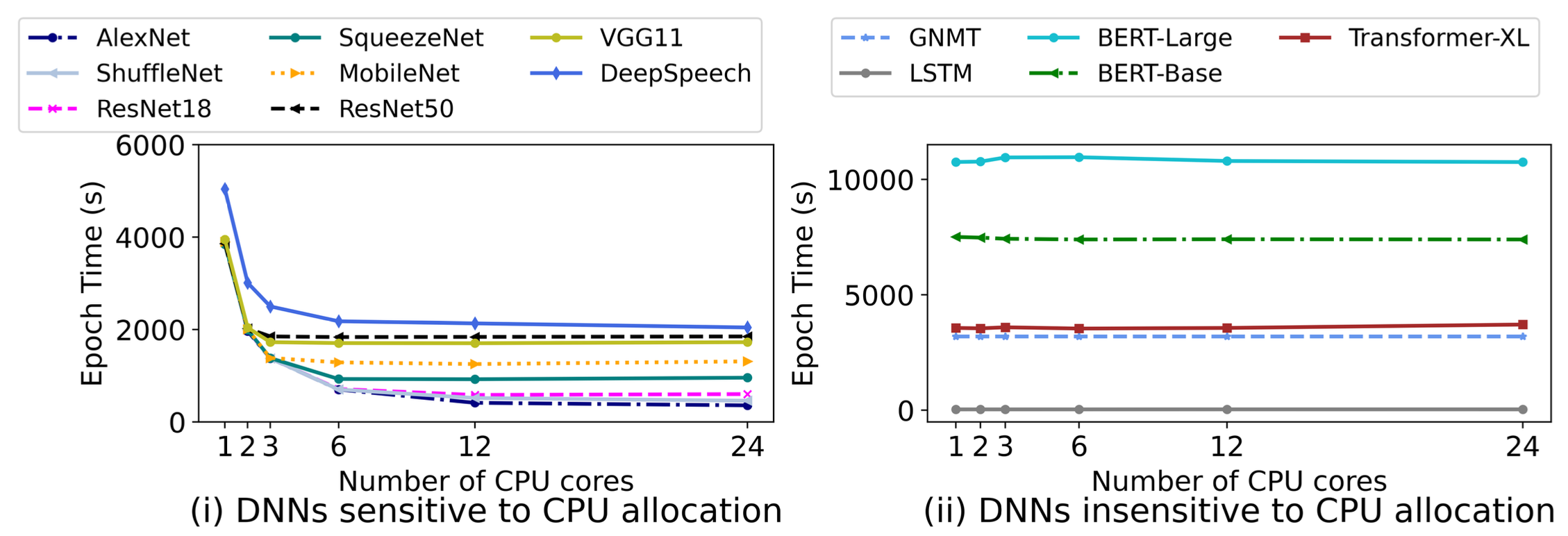
然而，作者发现，不同的 DNN 对于 CPU 和 MEM 呈现出了不同的 敏感性。 对于一些音视频识别的模型，当给他们分配的 CPU 和 MEM 多于 GPU-proportional allocation 时，可以取得接近 3 倍的加速。图 1 给出了一些案例。然而，对于一些自然语言处理模型（如 GNMT），即使给它们分配的 CPU 和 MEM 少于 GPU-proportional allocation，其训练速度也不会有明显的下降。不同的 DNN 对 MEM 也呈现出了不同的敏感性。

基于上述观测，作者提出了面向 同构的、多租户集群的调度器 Synergy，它能够很好地识别不同的 DNN 对 CPU 和 MEM 的敏感度，并给出精细化的分配方案。 具体地，Synergy 包含如下两个组成部分：

• 最优性分析（Optimistic Profiling）。 Synergy 测试并分析了在不同数量（多少）的 CPU 和 MEM 的组合下 DNN 训练任务的吞吐量。这个过程并非简单的枚举，而是使用了一些 trick 来降低计算量。分析结果对 CPU 和 MEM 的最优分配起到了重要作用。
• 调度机制（Scheduling Mechanism）。 在每一个调度周期，Synergy 首先识别出可以被调度的任务，然后基于上一阶段的分析给出 CPU 和 MEM 在不同任务上的划分策略（这种策略可以保证任务的吞吐量至少不少于 GPU-proportional allocation）。

2 Synergy 的设计架构

接下来我们依次介绍 Synergy 的最优性分析和调度机制。需要注意的是，Synergy 仅仅负责 CPU 和 MEM 的最优分配，GPU 的分配则直接采用用户指定的数量 ¹。

2.1 最优性分析

对于每一种提交的作业，Synergy 构造了一个 资源敏感性矩阵（resource sensitivity matrix）。如图 2 所示，这个矩阵试图记录不同的资源组合下的 DNN 训练任务的吞吐量。显然，如果要遍历每一种可能的组合并测试当前组合下的吞吐量是不现实的。为此，作者提出了一种基于 MinIO 的评估方案。MinIO 作为一种应用级别的缓存，可以保证一个 DNN 训练任务在每个 epoch 中拥有相同的缓存命中率， 这意味着，对于给定的 CPU 数量和存储带宽，我们可以建立吞吐量关于 MEM 数量的解析模型。因此，对于每一个 DNN，我们只需要将 MEM 固定为最大值，然后测试不同的 CPU 对吞吐量的影响即可（其他 MEM 数值下的吞吐量根据模型预测得到）。图 4 中的 empirical 和 estimated 正反应了这一点。

此外，其实也没有必要对每一个可分配的 CPU 数量都进行测试。为此，作者采用了一种基于 二分搜索 的测试方案——如果当前测试点的吞吐量增长少于某个阈值（例如 10%），则在 CPU 数量较少的这半区继续二分搜索；否则在 CPU 数量较多的这半区进行。

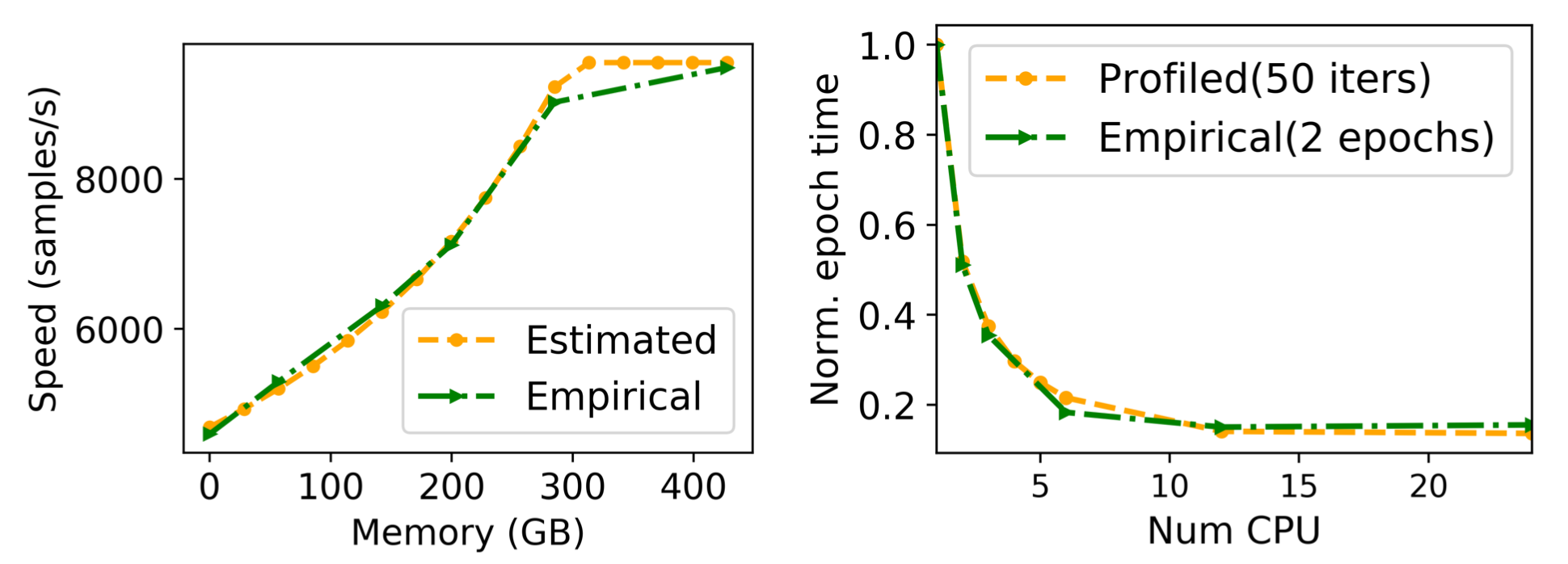
图 3 的实验结果表明针对 MEM 的预测模型和针对 CPU 的二分搜索可以很好地模拟实际情况。

2.2 调度机制

在每一个调度周期内，Synergy 首先从队列中获取可以被调度的任务，然后为每一个任务创建一个需求向量（demand vector）。该向量包含了当前任务的 GPU 需求量，以及满足吞吐量需求的最小数量的 CPU 和 MEM 数值 ²。根据这些需求向量将任务们分发到满足需求的节点上，这是一个 多维的装箱问题（multi-dimensional bin packing problem） ³。如果我们仅仅是设计一个贪心策略，即：依次对每一个可调度的任务，随机选择一个满足需求的节点，将其分发至该节点上，那么就不得不面临 资源碎片化 和 不公平分配 的问题。为了设计出一个具有理论性能保障的调度策略，作者进行了一些理论上的探索。我将在下一章节呈现作者的探索过程。

3 Synergy 的调度策略

3.1 理论最优解

作者做了一些理论上的探索 ⁴。首先，我们不妨假设只有一个节点，该节点装备有 $G$ 个单位的 GPU，$C$ 个单位的 CPU，以及 $M$ 个单位的 MEM。我们将第 $t$ 个调度周期中可被调度的 DNN 训练任务的集合记为 $J_t$。对于每一个任务 $j \in J_t$，不妨假设其 GPU 需求为 $g_j$。

我们在第 $t$ 个调度周期的决策变量为 $\vec{y} := \big[y_{c,m,j}\big]_{\forall c, m, j} \in \{ 0, 1 \}^{\forall c, m, j}$，其中的 $c$ 和 $m$ 分别遍历自资源敏感性矩阵。 若 $y_{c,m,j} = 1$，则意味着第 $j$ 个任务被分配到了 $c$ 个单位的 CPU 和 $m$ 个单位的 MEM。 我们用 $W_j[c, m]$ 表示当分配 $c$ 个单位的 CPU 和 $m$ 个单位的 MEM 给任务 $j$ 时，该任务在单个调度周期内能够完成的 epoch 的数量。 此外，我们将 GPU-proportional allocation 策略下分得的 CPU 和 MEM 的数量记为 $C_j$ 和 $M_j$，即

$$ \begin{equation} \begin{aligned} \left\{ \begin{array}{l} C_j = \frac{C}{G} \times g_j, \\ M_j = \frac{M}{G} \times g_j. \end{array} \right. \end{aligned} \end{equation} $$

至此，在每个调度周期 $t$，我们可以形成如下整数线性规划（ILP）问题 $\mathcal{P}_1$：

$$ \begin{equation} \begin{aligned} \mathcal{P}_1: \max \sum_{j \in J_t} \sum_{c, m} W_j [c, m] \cdot y_{c, m, j} \qquad \quad \\ s.t. \left\{ \begin{array}{l} \sum_{j \in J_t} \sum_{c, m} c \cdot y_{c, m, j} \leq C, \\ \sum_{j \in J_t} \sum_{c, m} m \cdot y_{c, m, j} \leq M, \\ \sum_{c, m} y_{c, m, j} = 1, \forall c, m, \\ \sum_{c, m} W_j [c, m] \cdot y_{c, m, j} \geq W_j [C_j, M_j]. \end{array} \right. \end{aligned} \end{equation} $$

最后一个约束表明求解该 ILP 取得的解至少应当好于 GPU-proportional allocation。$\mathcal{P}_1$ 可以通过专业的求解器（例如 CPLEX 或者 CVXOPT）求解。我们不妨将 $\mathcal{P}_1$ 最优解得到的任务 $j$ 的最优 CPU 和 MEM 分配分别记为 $c_j^*$ 和 $m_j^*$。

注意，以上的分析是建立在 我们只有一个节点 的假设上的。不过，即使有多个节点，问题也不会很复杂。这是因为作者做了一个强假设——每个节点是同构的，具有相同的 GPU、CPU 和 MEM 装配量。 我们可以建立一个如下的线性规划问题：我们定义 $x_{ij} \in [0, 1]$ 用于表示 $g_j$ 在节点 $i$ 上的分配比例，目标为 $\min_{\vec{x}} \sum_{j \in J_t} \sum_{i \in \mathcal{S}} 1 \{ x_{ij} > 0 \}$，其中 $\mathcal{S}$ 是节点的集合。这个目标是为了最小化不同节点上运行着的任务组件的通信开销尽可能低。这个 LP 问题看起来很难，实则很简单，因为对于任意任务 $j$，得益于节点的同构性，必然有 $x_{i_1, j} = x_{i_2, j}, \forall i_1, i_2 \in \mathcal{S}$。求解这个 LP 我们就可以得到每个任务在每个节点上的 GPU 分配量。 基于这个结果，我们只需要对每个节点求解一次上述的 ILP 即可。

至此，我们通过求解一个 LP 和数个 ILP，就得到了对于单个任务的、最优的 CPU 和 MEM 的分配方案。作者将这个调度策略命名为 Synergy-OPT。显然，Synergy-OPT 也可以被扩展到 异构 节点的场景中，此时第二个 LP 问题的计算会变得棘手且耗时。

3.2 Synergy 的实现方案

Synergy-OPT 存在两个无法忽视的问题：

• 求解这两个规划问题过于耗时；
• 第二个 LP 的求解会导致任务在单个节点上分配到非整数的 GPU 个数，例如 3.3 个 GPU。考虑到当前 GPU sharing 技术不是很成熟，我们不得不采用 rounding 的策略将其转化为整数解（例如，$3.3 \to 3$），这就必然会带来性能损失。

因此，作者又提出了一个叫做 Synergy-TUNE 的启发式策略，该策略遵循如下规则：

1. 只请求单个 GPU 的任务，我们必须将其分发至单个节点（不对任务做切分）；
2. 请求多个 GPU 的任务，可以被分发至单个节点，也可以被分发至多个节点（不同节点上启动的该任务的进程需要定期做 local gradients synchronization）。如果该任务被分发至多个节点，那么每个节点上 CPU 和 MEM 的分配遵循 GPU-proportional allocation 规则。 这样可以保证每个节点上的进程之间的进度不会差距过大，否则同步操作的耗时会增加。

在每个调度周期内，Synergy-TUNE 从待调度任务队列中依次取出 每一个 其 GPU 请求可以被满足的任务，然后按照 “先 GPU、后 CPU、最后 MEM” 的顺序对这些任务从大到小排序。接下来，从这个排好序的队伍中，Synergy-TUNE 依次取出每一个任务，计算其最优的 CPU 和 MEM 请求量，然后 在遵循上述两个规则的前提下 执行如下操作：

• 步骤 1： 如果这是一个 single-GPU 任务，Synergy-TUNE 将为其选择一个「满足其 GPU 需求的、资源余量 最少 的」节点；
• 步骤 2： 如果不存在单个节点能够满足其 GPU 请求，则尝试寻找 最少的 一组节点，使得该任务三个维度的资源需求都能够满足。
• 步骤 3： 如果整个集群的可用资源都不能满足这个任务，则执行如下操作：
  • 步骤 3.1： 如果当前任务的 CPU 和 MEM 请求量大于 GPU-proportional allocation 的结果，则将其 CPU 和 MEM 请求量置为 GPU-proportional allocation，然后依次重试步骤 1 和步骤 2；否则进入步骤 3.2；
  • 步骤 3.2： 如果一个任务无法被集群满足，或者其 CPU 和 MEM 请求量 小于等于 GPU-proportional allocation 的结果，则执行如下操作：找到一个满足其 GPU 请求的节点，然后将该节点上正在运行的任务们依次切换到 GPU-proportional allocation 模式（从而释放出一定的 CPU 和 MEM 资源），直到当前任务的 CPU 和 MEM 请求可以被满足为止。

通过执行以上操作，Synergy-TUNE 至少可以保证其性能不亚于 GPU-proportional allocation。

本文不再对 Synergy 的具体实现做介绍。

4 总结

这篇论文的 motivation 是：不同 DNN 训练任务对 CPU 和 MEM 这两个 “二等资源” 的分配量具有不同的敏感度，于是作者充分利用了它们在敏感度上的差异使得集群资源利用效率得以提高。Synergy 中的主要调度算法是 Synergy-TUNE，这只是一个简单的 heuristic，而且 在集群资源整体受限的情况下，很容易退化成 GPU-proportional allocation 策略。因此，可以预料得到，Synergy-TUNE 在大多数资源受限的集群条件下，应该不会有很明显的性能提升。

本文所有图片均截取自这篇论文。

转载申请

本作品采用 知识共享署名 4.0 国际许可协议 进行许可，转载时请注明原文链接。您必须给出适当的署名，并标明是否对本文作了修改。