树、二叉树及相关算法 · 数据结构与算法 01

树和图是十分重要的数据结构。在树和图上的操作（如层序遍历、深度优先遍历、寻找最短路、给出拓扑排序、判断是否连通等）在大型工程项目中频繁出现。本文作为数据结构与算法的第一篇文章，将重点关注树及相关常见操作的实现。本文不会重复树的基本理论，而是会以算法竞赛的风格对树的相关操作代码进行分析。 需要注意的是，尽管本文提到的仅仅是在树上的最常见操作，但彻底掌握它们仍然不是一件容易的事情。

1 树和二叉树

二叉树（binary tree）本身的定义就是 递归 的：

二叉树（定义。二叉树要么为空，要么由根节点（root）、左子树（left subtree）和右子树（right subtree）组成。而左子树和右子树分别是一棵二叉树。

树的定义和二叉树类似，区别是：在树中，每个节点不一定只有两棵子树。可以预见，树的内容会大量结合递归。正确理解并使用递归是掌握本文所涉及的代码的重要基础。

1.1 二叉树的编号

如图 1 所示，我们通常将二叉树的节点按照从上到下、从左到右的方式编号。如果一棵二叉树的所有叶子结点的深度都相同，则称这棵二叉树为 完全二叉树。

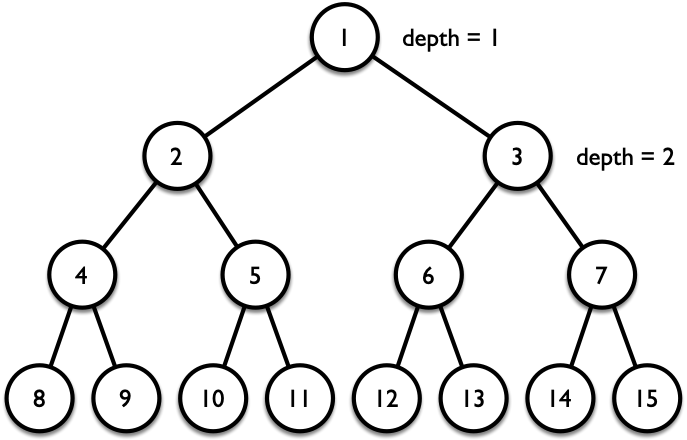
完全二叉树的节点编号（结论）。给定一棵包含 $2^d - 1$ 个节点的完全二叉树（$d$ 为二叉树的深度），将其节点从上到下、从左到右依次编号为 $1$、$2$、$3$、$\cdots$、$2^d - 1$，则对于一个编号为 $k$ 的节点，其左子节点和右子节点的编号分别为 $2k$ 和 $2k + 1$。

基于这个结论，我们就可以解决下面这道题目了。

例题 1：小球下落（Dropping Balls, UVa 679）

有一棵深度为 $D$ 的完全二叉树（$D \leq 20$），所有节点从上到下、从左到右依次编号为 $1$、$2$、$3$、$\cdots$、$2^D - 1$。在节点 $1$ 处放一颗小球，它会往下落。每个内节点上都有一个开关，初始全部关闭，每当有小球落到一个开关上时，开关的状态首先会改变。然后，如果改变前的状态为「关闭」，则小球往左走，否则小球往右走，直到走到叶子结点。假设一共有 $I$ 个小球，求第 $I$ 个小球最后所在的叶子编号。

我们将 maxn 定义为大小为 20 的常量，用于描述最大的树深度，用大小为 1 << maxn 的 int 数组 s 来存储每一个节点（开关）。 则可以写出如下模拟代码：

// D 和 I 已经从标准输入中读取
int k;                      // k 为小球当前所在节点编号
int n = (1 << D) - 1;       // n 为节点最大编号
memset(s, 0, sizeof(s));
// 模拟 I 次小球下落
for (int i = 0; i < I; i++) {
    k = 1;
    while (true) {
        s[k] = !s[k];
        if (s[k] == 1) {
            k = 2 * k;
        } else {
            k = 2 * k + 1;
        }
        if (k > n) break;
    }
}
printf("%d\n", k / 2);      // k / 2 为出界前的节点编号

完整代码请参见 aoapc/ch06/e6-6-1。

以上代码基于对小球下落行为的模拟。当 $D$ 接近 20 的时候，这是一笔极大的运算开销。 有没有更高效的方法呢？我们应该透过模拟行为去观察问题的本质。首先，每一颗小球都从根节点开始下落。这意味着第「奇数」个小球必然进入根节点的左子树，第「偶数」个小球则进入根节点的右子树。对于每一棵子树而言，我们只需要知道当前进入这棵子树根节点的小球是第奇数个还是第偶数个，就知道它是往左走还是往右走了。经过探索和归纳，可以发现，对于编号为 $I$ 的小球：

• 当 $I$ 是奇数时，它往根节点的左边走，并且它是进入根节点左子树的第 $\frac{I + 1}{2}$ 个小球；
• 当 $I$ 是偶数时，它往根节点的右边走，并且它是进入根节点右子树的第 $\frac{I}{2}$ 个小球。

进入左右子树之后，再按照同样的逻辑去分析，直到我们抵达叶子结点。显然，我们是需要循环的。因为完全二叉树的深度为 $D$，所以我们只需要循环上述操作 $D$ 次，即可抵达叶子结点。由此，我们可以直接写出如下代码：

// D 和 I 已经从标准输入中读取
int k = 1;                  // k 为小球当前所在节点编号
int n = (1 << D) - 1;       // n 为节点最大编号
for (int i = 0; i < D; i++) {
    if (I % 2 == 1) {
        k = 2 * k;
        I = (I + 1) / 2;
    } else {
        k = 2 * k + 1;
        I = I / 2;
    }
}
printf("%d\n", k);

完整代码请参见 aoapc/ch06/e6-6-2。 这相当于我们已经洞悉了每一颗小球的下落模式，然后直接模拟了最后一颗小球的下落。这样，我们不仅省下了一个大数组 s，而且节省了巨大的运算量。

1.2 二叉树的实现与层序遍历

在我们的固有印象中，二叉树是需要通过「结构体 + 指针」的方式来实现的。 定义一棵二叉树，首先需要定义一个节点类型的结构体。在这个结构体中，我们需要定义当前节点内存放的数据（可以是任意类型，包括自定义结构体），以及指向左右子节点的指针。然后我们需要申明全局的根节点 root。下面给出了一种存储 int 数据的标准实现：

struct Node {
    bool have_value;
    int val;
    Node *left, *right;

    Node() : have_value(false), val(0), left(nullptr), right(nullptr) {}
};

Node *root;

在 C++ 中，我们使用 new 和 delete 运算符申请和释放内存空间，其中 new 运算符在内部会自动调用结构体提供的、对应的构造函数，返回指向新申请的空间的首地址指针。对于二叉树而言，我们要如何释放它所占用的空间呢？显然，我们需要按照从叶子结点到根节点的顺序进行释放。这是因为释放占用空间的本质是丢弃指向特定空间的指针，从而让这块空间可以被其他程序写入。如果我们先丢失了指向根节点的指针，则左右子树的空间并未被释放，但是我们再也找不到它们了，这就造成了 内存泄露——有些内存空间被白白浪费了。虽然语言的运行时通常有垃圾回收机制来处理这些问题，但是我们应该尽量避免制造内存泄露。联想树的递归定义，我们可以通过递归函数调用来实现其空间释放：

Node *new_node() {
    return new Node();
}

void remove_tree(Node *u) {
    remove_tree(u->left);
    remove_tree(u->right);
    delete u;
}

接下来，我们基于「结构体 + 指针」的方式建树。

例题 2：树的层序遍历（Trees on the level, Duke 1993, UVa 679）

输入一棵二叉树，每个节点都按照从根节点到到它的移动序列给出（L 表示左，R 表示右）。以 () 结束。请按照从上到下、从左到右的顺序输出各节点存储的数值。

样例输入： (11,LL) (7,LLL) (8,R) (5,) (4,L) (13,RL) (2,LLR) (1,RRR) (4,RR) ()
样例输出： 5 4 8 11 13 4 7 2 1

建树中，我们首先需要创建根节点，然后，依次将给定的节点插入到树中合适的位置上。我们需要读取这个节点的移动序列，沿着左子树或右子树一路南下，通过设定它的父节点的 left 或 right 指针来建立父子关系。就本问题而言，读取移动序列的部分如下：

char s[300];                    // 存放读入的移动序列

void read_input() {
    root = new_node();          // 创建根节点
    for (;;) {
        if (!strcmp(s, "()")) break;
        int val;
        sscanf(&s[1], "%d", &val);
        // 以 (2,LLR) 为例，2 被读入 val 中，
        // "LLR)" 作为第二个参数被传递给了 add_node() 函数
        add_node(val, strchr(s, ',') + 1);
    }
}

接下来，我们将给定的节点插入到树中合适的位置上。这部分代码非常重要，几乎所有的建树代码都与其相似，需要彻底掌握。

bool add_node(int val, char *s) {
    int n = (int) strlen(s);
    Node *u = root;
    // 下面的代码意味着，我们将沿途经历过的、尚未创建的节点都一并创建了
    for (int i = 0; i < n; i++) {
        if (s[i] == 'L') {
            if (u->left == nullptr) {
                u->left = new_node();
            }
            u = u->left;
        } else if (s[i] == 'R') {
            if (u->right == nullptr) {
                u->right = new_node();
            }
            u = u->right;
        }
    }
    if (u->have_value) {
        return false;
    }
    // u 此时指向本节点，为其设定数值
    u->val = val;
    u->have_value = true;
    return true;
}

至此，一棵树已经根据输入序列建立完毕。接下来我们要按照从上到下、从左到右的顺序将每个节点的数值打印出来。这个过程被称为层序遍历（又称宽度优先遍历，BFS）。BFS 在各种显式图和隐式图中扮演着重要角色，需要彻底掌握。

这样，我们就保证了处于同一个深度的节点在队列中是相邻的，从而实现「宽度优先」的遍历。代码如下：

// 我们将结果存入一个 vector 中
void bfs(vector<int> &res) {
    res.clear();

    queue<Node *> q;
    q.push(root);
    while (!q.empty()) {
        Node *u = q.front();
        q.pop();
        res.push_back(u->val);
        if (u->left != nullptr) q.push(u->left);
        if (u->right != nullptr) q.push(u->right);
    }
}

完整代码请参见 aoapc/ch06/e6-7-1。

二叉树是否一定要用「结构体 + 指针」的方式来实现？实际上，我们使用指针的本质原因是每个节点可能被存放在不连续的内存空间中，因此需要一种方式来寻址，而指针就是绝佳的寻址工具。不过，除了指针，数组也可以被用来寻址。我们可以给每个节点依次编号为 $1$、$2$、$\cdots$，用数组 left 和 right 存放每个节点的左孩子编号和右孩子编号，用数组 values 存放每个节点内存放的数值。数组的下标和节点的编号一一对应。基于此，我们可以将二叉树按照如下方式实现：

// 用 cnt 表示当前已存在的节点编号的最大值
// 用 left 和 right 数组分别表示每个节点的左孩子和右孩子的编号（注意区分节点的编号和节点中存放的数值）
// 用 values 数组记录每一个节点中存放的数值
// 用 have_value 数组记录每一个节点是否已经被赋值
const int maxn = 256;
int cnt;
int left[maxn], right[maxn], values[maxn];
bool have_value[maxn];

const int root = 1;

// 只需要重置计数器和根节点的左右子树即可清空整棵树
void new_tree() {
    left[root] = right[root] = 0;
    have_value[root] = false;
    cnt = root;
}

// 创建一个节点，只需要初始化其左右子树即可。返回的是当前节点的编号
int new_node() {
    int u = ++cnt;
    left[u] = right[u] = 0;
    have_value[u] = false;
    return u;
}

因为数组可以随便复写，因此不需要 remove_tree() 这样的函数来销毁一个树。实际上，new_tree() 同时执行了清空旧树和创建新树的操作。对于以数组形式实现的二叉树，如何添加节点呢？整体上只需要仿照上面的 add_node() 实现即可：

bool add_node(int val, char *s) {
    int n = (int) strlen(s);
    int u = root;
    for (int i = 0; i < n; i++) {
        if (s[i] == 'L') {
            if (left[u] == 0) {
                int lc_idx = new_node();
                left[u] = lc_idx;
            }
            u = left[u];
        } else if (s[i] == 'R') {
            if (right[u] == 0) {
                int rc_idx = new_node();
                right[u] = rc_idx;
            }
            u = right[u];
        }
    }
    if (have_value[u]) {
        return false;
    }
    // u 此时指向本节点，为其设定数值
    values[u] = val;
    have_value[u] = true;
    return true;
}

同理，可以实现数组版本的 BFS：

bool bfs(vector<int> &res) {
    res.clear();

    queue<int> q;
    q.push(root);
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        res.push_back(values[u]);
        if (left[u]) q.push(left[u]);
        if (right[u]) q.push(right[u]);
    }
}

完整代码请参见 aoapc/ch06/e6-7-2。

虽然用数组实现二叉树更简单（因为不涉及到指针操作），但是访问速度比指针慢。在工程实践中，有一种重要的处理思路，叫做「动态化静态」——用静态数组配合空闲列表来实现一个内存池。当需要创建新节点时，从内存池中取出一个节点，填充进数值；当需要释放它的时候，将其塞回内存池即可。下面是这种思想的实现：

struct Node {
    bool have_value;
    int val;
    Node *left, *right;

    Node() : have_value(false), val(0), left(nullptr), right(nullptr) {}
};

Node *root;

const int maxn = 256;
Node nodes[maxn];                   // 静态申请的结构体数组
queue<Node *> free_nodes;           // 空闲节点列表

// 初始化内存池
void init() {
    for (auto &node : nodes) {
        free_nodes.push(&node);
    }
}

// 创建一个新的 node，本质上就是从内存池中申请一个 node 空间占用
Node *new_node() {
    Node *u = free_nodes.front();
    u->left = u->right = nullptr;
    u->have_value = false;
    free_nodes.pop();
    return u;
}

// 释放一个 node，本质上就是将其放回空闲内存池中
void delete_node(Node *u) {
    free_nodes.push(u);
}

add_node() 和 bfs() 和基于「结构体 + 指针」的实现方式完全相同。完整代码请参见 aoapc/ch06/e6-7-3。

至此，我们阐述了三种实现二叉树的方式。分别是基于「结构体 + 指针」的模式、基于「数组」的模式和基于「静态数组 + 空闲列表」的模式。其中第一种模式最常见；第二种模式无法扩展到一般的树，但是实现和 debug 简单；第三种模式在高水平算法竞赛和工程实践中极为重要。对于每一种实现，我们都给出了根据移动序列建树和 BFS 的实现。

这一部分的内容需要熟练掌握。

1.3 二叉树的深度优先遍历

对于一棵二叉树 T，我们可以递归定义它的先序遍历、中序遍历和后序遍历分别如下：

• PreOrder(T) = T 的根节点 + PreOrder(T 的左子树) + PreOrder(T 的右子树)
• InOrder(T) = InOrder(T 的左子树) + T 的根节点 + InOrder(T 的右子树)
• PostOrder(T) = PostOrder(T 的左子树) + PostOrder(T 的右子树) + T 的根节点

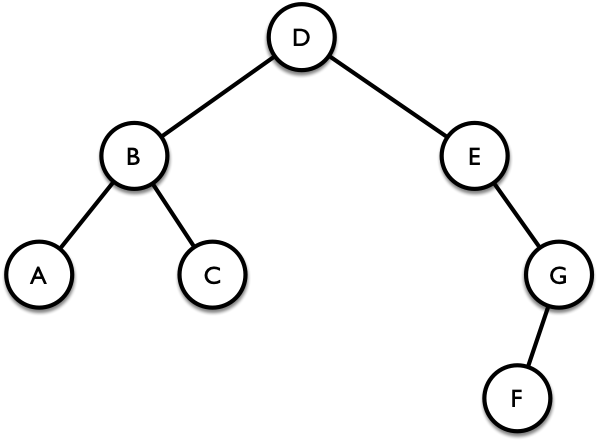
这三种遍历被称为深度优先遍历（DFS），因为它们总是优先往深处访问。 对于图 2 所示的二叉树，其先序遍历为 DBACEGF，中序遍历为 ABCDEFG，后序遍历为 ACBFGED。

接下来，我们就一个例题给出根据中序遍历和后序遍历建树的代码。

例题 3：树（Tree, UVa 548）

给出一棵点带权的二叉树的中序遍历和后序遍历，找出叶子节点使得它到根的路径上的权和最小。如果有多解，则该叶子节点本身的权应尽量小。

样例输入：
7 8 11 3 5 16 12 18
8 3 11 7 16 18 12 5

样例输出：3

对于这个问题，首先我们需要把树构建出来，然后执行一次 DFS 找到最优解。我们使用数组存储树：

// 直接用节点的权值作为节点的编号（省下一个数组的空间）
const int maxn = 10000 + 10;
int left[maxn], right[maxn];

// 存放中序遍历和后续遍历
int in_order[maxn], post_order[maxn];

要做的第一件事，是读取中序遍历和后序遍历并将它们存入数组中。我们使用 getline() 函数结合 stringstream 来做到这一点：

int n;              // 节点个数

// 如果什么数字也没读到，返回 false
bool read(int *a) {
    string line;
    if (!getline(cin, line)) return false;
    stringstream ss(line);
    n = 0;
    int x;
    while (ss >> x) {
        a[n++] = x;
    }
    return n > 0;
}

这样，我们只需要通过函数调用 read(in_order) 和 read(post_order) 就可以将遍历结果存入这两个数组中。

接下来是最重要的部分，即通过递归调用的方式构建树。 那么，这个递归函数要如何设计呢？首先，它的参数必然和两个数组 in_order、post_order 有关。各个递归调用栈最显著的区别是，它们将使用这两个数组不同的、某个连续子部分。而在函数内部，应该清晰地计算出下一次递归调用应该使用哪些子部分。因此，一种自然而然的设计是将 4 个 int 变量作为参数，分别为本次递归调用所使用的 in_order 和 post_order 的子部分的首尾索引。这个递归函数是否需要有返回值？如果有，应当返回什么？一种设计是，返回当前子树的根。这个根必然是前一次调用的左孩子或右孩子。返回当前子树的根可以让我们直接建立节点之间的父子关系。

基于上述分析，我们可以写出如下代码：

// in_order[L1...R1] 和 post_order[L2...R2] 是我们关注的连续子部分
int build_tree(int L1, int R1, int L2, int R2) {
    if (L1 > R1) return 0;      // 空树
    // cur_root 是权值，但是 left[cur_root] 和 right[cur_root] 又将其用作索引
    // 我们就是这样节省了一个权值数组 values[maxn] 的
    int cur_root = post_order[R2];
    int p = L1;
    // 在中序遍历中找到根的位置
    while (in_order[p] != cur_root) p++;
    int left_node_num = p - L1;
    left[cur_root] = build_tree(L1, p - 1, L2, L2 + left_node_num - 1);
    right[cur_root] = build_tree(p + 1, R1, L2 + left_node_num, R2 - 1);
    return cur_root;
}

这个实现非常重要，必须要熟练掌握。

当我们把树构建出来之后，只需要来一遍 DFS 即可找到最优的叶子节点。 DFS 不同于 BFS（用队列实现），它用递归实现。如何递归呢？设 dfs(u) 表示从节点 u 开始到某个叶子节点的权值之和，则 dfs(u) = values[u] + dfs(u->left) 或 dfs(u) = values[u] + dfs(u->right)，这样设计的函数 dfs() 需要返回一个 int 类型的变量。按照上面的方式实现一下：

int dfs(int u) {
    // u 是叶子结点
    if (!left[u] && !right[u]) {
        return u;
    }
    if (left[u]) {
        return u + dfs(left[u]);
    }
    if (right[u]) {
        return u + dfs(right[u]);
    }
}

读者可以试试调用这个函数实现会发生什么。它只会给出一个和，并且，这个和是从二叉树的根一路沿着右孩子南下，直到 “最后一个「是其父节点的右孩子」的叶子节点” 或 “最后一个没有右孩子的非叶节点”。它缺少对所有可能的和的遍历，显然不能给出我们想要的答案。

更好的方式是将到目前为止的权值之和也作为参数传递给 dfs() 函数，一旦抵达叶子结点，就进行清算——判断当前和（作为一个可行解）和到目前为止记录的最优解哪个更好并更新最优解。基于此的函数实现如下：

int best_u, best_sum = 1000000;

void dfs(int u, int cur_sum) {
    cur_sum += u;
    // u 是叶子结点
    if (!left[u] && !right[u]) {
        // cur_sum 是一个可行解
        if (cur_sum < best_sum || (cur_sum == best_sum && u < best_u)) {
            best_u = u;
            best_sum = cur_sum;
        }
    }
    if (!left[u]) {
        dfs(left[u], cur_sum);
    }
    if (!right[u]) {
        dfs(right[u], cur_sum);
    }
}

最后，我们只需要把 best_u 输出即可。完整代码请参见 aoapc/ch06/e6-8。

上面给出了「根据中序遍历和后序遍历建树」的代码。实际上，根据先序遍历和中序遍历也能建树。整体结构类似——记住，先序遍历的第一个元素是（子）树的根即可。详情请参考 二叉树重建（Tree recovery, ULM 1997, UVa 536） 和 aoapc/ch06/p6-3。

例题 4：天平（Not so mobile, UVa 839）

输入一个树状天平，根据力矩相等原则判断是否平衡。力矩相等就是 $W_l D_l = W_r D_r$，其中 $W_l$ 和 $W_r$ 分别为左右两边砝码的重量，$D_r$ 和 $D_r$ 分别为左右两边砝码到立柱的距离。采用递归（先序）的方式输入：每个天平的格式为 $W_l, D_l, W_r, D_r$，当 $W_l$ 或 $W_r$ 为 $0$ 的时候，表示该 “砝码” 实际上是一个子天平，接下来会描述这个子天平。当 $W_l = W_r = 0$ 时，会先描述左子天平，后描述右子天平。

样例输入：
0 2 0 4
0 3 0 1
1 1 1 1
2 4 4 2
1 6 3 2

样例输出：YES

我们要找到问题中的关键点：输入是以递归的形式给出的。对于某个（子）天平，它是平衡的，当且仅当以下三个条件同时成立：

• 它的左子天平是平衡的；
• 它的右子天平是平衡的；
• 当前这个天平 “左砝码” 和 “右砝码” 是平衡的。

注意，对于任意一个（子）天平，如果它的左砝码是一个子天平，那么这个左砝码的重量为这个子天平中左右砝码的重量之和。右砝码的重量同理。由此，我们可以在处理输入的时候直接跟着一起递归——对于当前天平：

• 如果左砝码的重量为零，说明左砝码是一个子天平，递归调用自身判断左子天平是否平衡，并计算 “左砝码” 的重量；
• 如果右砝码的重量为零，说明右砝码是一个子天平，递归调用自身判断右子天平是否平衡，并计算 “右砝码” 的重量；
• 根据得到的左右砝码的重量，判断当前天平是否平衡。

当前天平是平衡的，当且仅当以上三个关于是否平衡的判断返回的都是 true。基于以上分析，我们可以写出如下代码：

bool solve(int &W) {
    int Wl, Dl, Wr, Dr;
    bool bl = true, br = true, b;
    cin >> Wl >> Dl >> Wr >> Dr;
    if (Wl == 0) {
        // 判断左子天平是否平衡，并计算 “左砝码” 的重量
        bl = solve(Wl);
    }
    if (Wr == 0) {
        // 判断右子天平是否平衡，并计算 “右砝码” 的重量
        br = solve(Wr);
    }
    // 根据得到的左右砝码的重量，判断当前天平是否平衡
    W = Wl + Wr;
    b = (Wl * Dl == Wr * Dr);
    // 当且仅当以上三个判断返回的均为 true
    return bl && br && b;
}

和上一题一样，这里我们将 “砝码重量” 这个需要计算的量作为参数引用传入递归函数中，而非作为递归函数的返回值。 完整代码请参见 aoapc/ch06/e6-9。

例题 5：下落的树叶（The falling leaves, UVa 699）

给一棵二叉树，每个节点都有一个水平位置：左子节点在它左边一个单位，右子节点在它右边一个单位。从左向右输出每个水平位置的所有节点的权值之和。如图 3 所示，从左到右的 4 个位置的权和分别为 9、7、21、15。按照递归（先序）方式输入，用 -1 表示空树。

样例输入：
8 2 9 -1 -1 6 5 -1 -1 12 -1 -1 3 7 -1 -1 -1

样例输出：
9 7 21 15

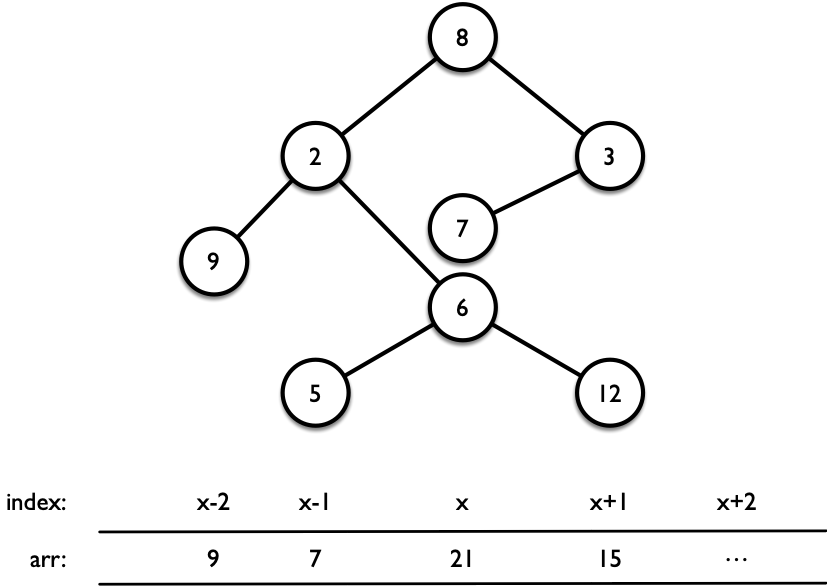
这题要如何解？首先，我们肯定需要一个数组 arr 来存储每个水平位置的权值和。我们应该尽量把树 “往数组的中间放”，即让根节点的水平位置在差不多数组的中间位置，这样左右两边的子树能分别放得下。我们需要一个递归函数 dfs() 来递归地更新数组 arr。这个递归函数的参数是什么？是否有返回值？我们将需要更新的变量作为递归函数的参数。 在本问题中，需要更新的量是每个节点的水平位置。对于任意一个给定的水平位置 p，我们应该执行如下操作：

1. 读入一个数值，将这个数值加到 arr[p] 上；
2. 因为输入采取先序遍历的方式给出，因此下一个节点会是当前节点的左孩子，所以我们递归调用 dfs(p-1)；
3. 然后处理右孩子：dfs(p+1)。

其中，在步骤 1 中，我们需要判断当前节点是否存在，如果读入的数值是 -1，说明当前节点不存在，直接退出本轮递归调用——既不需要加上什么数值，也不需要再检查这个节点的左右孩子了（因为没有）。由此，我们可以写出如下代码：

const int maxn = 10000;
int arr[maxn];

void dfs(int p) {
    int val;
    cin >> val;
    if (val == -1) return;
    arr[p] += val;
    dfs(p - 1);
    dfs(p + 1);
}

在第一次调用 dfs() 时，我们将 p 设定为 maxn / 2。完整代码请参见 aoapc/ch06/e6-10。

例题 6：Undraw the trees, UVa 10562）

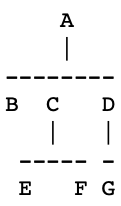
我们的任务是将一个树转化为括号表示法。参见图 4 所示的样例输入，每个节点用除了 -、| 和空格的其他字符表示，每个非叶节点的正下方总会有一个 | 字符，然后下方是一排 - 字符，恰好覆盖所有子节点的上方。 对于图 4 所示的输入，输出为 (A(B()C(E()F())D(G())))。

输入的是二维字符数组，我们需要在二维数组中递归。对于每个位置为 (i,j) 的字符：

• 如果这个字符代表的是一个节点，我们首先需要将其打印出来；
• 然后，我们需要判断位置 (i+1,j) 的元素是否为 |：
  • 若是，则说明本节点是非叶节点，在第 i+2 行找到 --- 的左边界，然后对于每个 - 下面（可能存在的）节点递归；
  • 若不是，则说明本节点是叶子节点，什么也不做。

下面给出了这种递归的实现：

const int maxn = 200 + 5;
char arr[maxn][maxn];               // 读取到的二维字符数组
int n;                              // 读取到的二维字符数组的真实行数

// 以字符 arr[r][c] 为（子）树的根递归建树
void dfs(int r, int c) {
    printf("%c(", arr[r][c]);
    if (r + 1 < n && arr[r + 1][c] == '|') {
        // 是非叶节点
        int j = c;
        // 找到 "---" 的左边界
        while (j - 1 >= 0 && arr[r + 1][j] == '-') j--;
        while (arr[r + 2][j] == '-' && arr[r + 3][j] != '\0') {
            if (!isspace(arr[r + 3][j])) {
                // 是一个节点，递归
                dfs(r + 3, j);
            }
            j++;
        }
    }
    printf(")");
}

对于上述 dfs() 的首次调用，我们需要在二维数组 arr 的第一行中找到树根所在的列。完整代码请参见 aoapc/ch06/e6-17。

1.4 一般树的深度优先遍历

一般的树在很多操作上和二叉树并没有什么不同。区别是一般树可能不具有二叉树的某些优美性质。

例题 7：四分树（Quadtrees, UVa 297）

如图 5 所示，我们用四分树来表示一个大小为 $32 \times 32$ 的黑白图像（一共 $1024$ 个像素点），方法是用根节点表示整幅图像，然后把行列各分成两等分，按照图中的方式编号，从左到右对应 4 个子节点。如果某子节点对应的区域全黑或者全白，则直接用一个黑节点或者白节点表示；如果既有黑又有白，则用一个灰节点表示，并且为这个区域递归建树。给出两棵四分树的先序遍历，求二者合并之后（黑色部分合并）黑色像素的个数。用 p 表示中间节点，f 表示黑色节点，e 表示白色节点。

样例输入：
ppeeefpffeefe
pefepeefe

样例输出：
There are 640 black pixels.

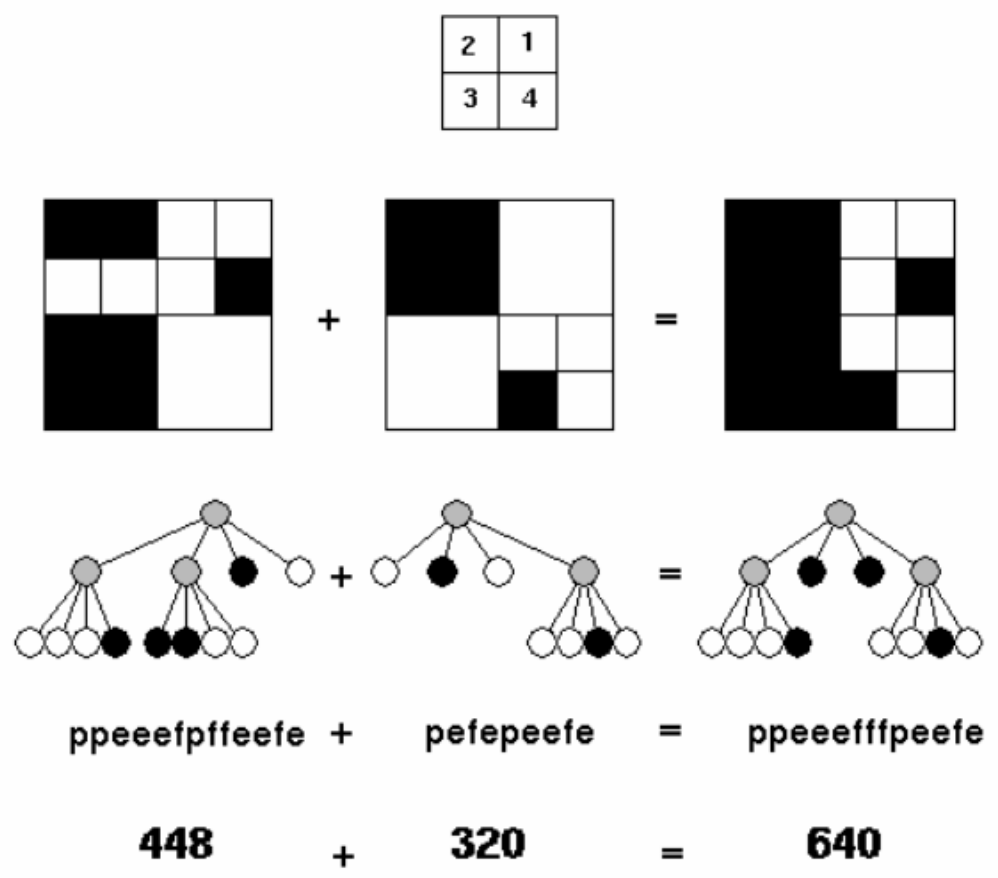
首先，我们肯定需要一个大小为 $32 \times 32$ 的二维数组来存储合并的结果，我们再用全局变量 cnt 来存储这个数组中黑色像素的个数。其次，我们需要一个字符数组来存储每一条先序遍历的输入。

const int maxn = 1024 + 5;
char s[maxn];
int arr[32][32];            // 存储 0 和 1，1 表示黑色像素
int cnt;

接下来，我们需要根据先序遍历建树。对于四分树而言，只需要先序遍历就可以构建出整棵树。这是因为每个非叶节点都有 4 个孩子。我们仍然将递归函数起名为 dfs()。首先，字符子串中第一个元素是根节点，我们需要判断它是 p、e 还是 f。

• 如果它是 p，意味着它有 4 个孩子节点，我们直接递归调用自身；
• 如果它是 f，我们需要把 arr 中对应的区域内的元素设定为 1。
• 如果它是 e，我们什么都不需要做。

现在，最大的问题是，如何将先序遍历中的字符子串和一棵子树（二维数组的某个特定的正方形区域）建立关联。 我们用 r 和 c 表示这个正方形区域的起始行列索引，用 w 表示这个正方形区域的宽度，则我们可以将 dfs() 申明为：

void dfs(char *s, int &start, int r, int c, int w);

其中 start 记录了本次递归调用的子串首地址。根据以上分析，我们可以写出如下代码：

void dfs(char *s, int &start, int r, int c, int w) {
    char ch = s[start];
    start++;
    if (ch == 'p') {
        dfs(s, start, r, c + w / 2, w / 2);
        dfs(s, start, r, c, w / 2);
        dfs(s, start, r + w / 2, c, w / 2);
        dfs(s, start, r + w / 2, c + w / 2, w / 2);
    } else if (ch == 'f') {
        for (int i = r; i < r + w; i++) {
            for (int j = c; j < c + w; j++) {
                if (buf[i][j] == 0) {
                    buf[i][j] = 1;
                    cnt++;
                }
            }
        }
    }
}

我们分别两次将两棵四分树的先序遍历读入字符数组 s 中，并分别调用一次 dfs(s, 0, 0, 0, 32) 即可得到最终的 arr 和 cnt。最后输出 cnt 即可。完整代码请参见 aoapc/ch06/e6-11。

另一道跟四分树有关的题是 空间结构（Spatial structures, ACM/ICPC World Finals 1998, UVa 806），没有涉及超出本题的知识点。对应的解决方案参见 aoapc/ch06/p6-8。

2 一些思考题

例题 8：修改天平（Equilibrium mobile, NWERC 2008, UVa 12166）

给一棵深度不超过 16 的二叉树，代表一个天平。每根杆都悬挂在中间，每个秤砣的重量已知。至少修改多少个秤砣的重量才能让天平平衡？对于图 6 所示天平，将 7 改成 3 即可。

样例输入：
3
[[3,7],6]
40
[[2,3],[4,5]]

样例输出：
1
0
3

要修改尽可能少的秤砣，这意味着我们应该让 “价值量” 出现次数最多的秤砣们保持不变，而去修改别的秤砣。可是，每个秤砣的价值量如何衡量呢？可以用它「相对根节点」的重量。对于每个叶子节点而言，若它的重量为 w，深度为 level，则它相对于根节点的重量为 w << level。由于输入是以递归的形式给出的，因此本题的难点是如何结合递归计算每种价值量的秤砣出现的次数。对应的代码实现如下：

string s;                       // 存放读入的字符串
map<long long, int> values;     // 存放叶子的 value 到出现次数的映射
int leaf_num, max_value;

// s[begin, begin + len] 对应一棵深度为 level 的子树
void dfs(int level, int begin, int len) {
    if (s[begin] == '[') {
        int p = 0;
        for (int i = begin + 1; i < len; i++) {
            // 下面两行是为了确保找到当前深度的前后两个子树
            if (s[i] == '[') p++;
            if (s[i] == ']') p--;
            // p 为 0 意味着'['和']'成对出现，即能跨越一个（或多个）完整的子树
            if (p == 0 && s[i] == ',') {
                // 逗号分开了左右子树，分别递归
                dfs(level + 1, begin + 1, i - 1);
                dfs(level + 1, i + 1, len - 1);
            }
        }
    } else {
        // 不是'[', ']', '.'，则只能是数字，即叶子节点的值
        long long w = 0;
        for (int i = begin; i <= len; i++) {
            w = w * 10 + s[i] - '0';
        }
        // cnt 记录了叶子结点的数量
        leaf_num++;
        // value 的计算方式：从当前叶子节点溯源至 root，即 w * 2^level
        values[w << level]++;
        max_value = max(max_value, values[w << level]);
    }
}

完整代码请参见 aoapc/ch06/p6-6。

例题 9：树重建（Tree reconstruction, UVa 10410）

输入一棵有 $n$ 个节点的树的 BFS 和 DFS 序列，输出每个节点的子节点列表。输入序列（不论是 BFS 还是 DFS）是这样生成的：当一个节点被扩展时，其所有子节点应该按照编号从小到大的顺序访问。例如，若 BFS 序列为 4 3 5 1 2 8 7 6，DFS 序列为 4 3 1 7 2 6 5 8，则一棵满足条件的树如图 7 所示。

这道题要如何求解？我们可以拿 DFS 的序列，分成若干段，每一段相当一个子树，这样就可以利用 BFS 的序列去将 DFS 的序列分段，然后利用一个队列去存放每一段，不断求出子树即可。为此，我们首先需要准备如下数据结构：

const int maxn = 1000 + 5;
int n;                          // 节点个数
int BFS[maxn], DFS[maxn];       // BFS 和 DFS 的序列（从 index = 0 开始存储）
int cur;                        // 当前游标所在位置
vector<int> children[maxn];     // 存放结果。从 1 开始计数

// 用于标识 DFS 序列中的一个子段
struct Seq {
    int l, r;   // [l, r)
    Seq(int l, int r) : l(l), r(r) {}
};

然后，我们基于 BFS 框架实现上述思路：

// 从 DFS 序列中得到一个个分段（子树）
void bfs() {
    cur = 1;
    queue<Seq> q;
    q.push(Seq(0, n));
    while (!q.empty()) {
        Seq s = q.front();
        q.pop();
        int u = DFS[s.l];
        if (cur == n || s.l + 1 == s.r) continue;
        // 在 DFS new_l 紧跟着 u，因此 new_l 必然是 u 的孩子
        int new_l = s.l + 1;
        children[u].push_back(DFS[new_l]);              // 这里是直接记录孩子节点的代码
        cur++;      // BFS[cur] 是当前根 u 的下一个孩子，我们要在 DFS 序列中找到它
        for (int new_r = s.l + 2; new_r < s.r; new_r++) {
            // 在 DFS 序列中找到 u 的下一个直接孩子节点 DFS[new_r]
            if (BFS[cur] == DFS[new_r]) {
                children[u].push_back(DFS[new_r]);      // 这里是直接记录孩子节点的代码
                // new_l 和 new_r 分别是 u 的前后相邻的两个孩子的 index
                // 因为可能是多叉树，所以更新 new_l 为 new_r，再继续找下一个孩子的 index new_r（如果有的话）
                q.push(Seq(new_l, new_r));
                new_l = new_r;
                cur++;
            }
        }
        if (new_l < s.r) {
            // 这一部分是最后一棵子树（从最后一个孩子的 index 到序列末尾）
            q.push(Seq(new_l, s.r));
        }
    }
}

完整代码请参见 aoapc/ch06/p6-11。

3 总结

本文重点解析了树和二叉树的建立和遍历的代码。树的层序遍历总可以用队列来实现，而树的深度优先遍历和递归紧密关联。如何设计好递归函数从而解决与树相关的问题，是本文试图传达的重要信息。本文所有列出的代码都十分重要，建议读者完全掌握。

最后

本文改写自刘大爷的经典教材《算法竞赛入门经典（第二版）》的第六章的部分内容。此外， 图 5 来自 UVa 的官方网站：UVa 297。

转载申请

本作品采用 知识共享署名 4.0 国际许可协议 进行许可，转载时请注明原文链接。您必须给出适当的署名，并标明是否对本文作了修改。