对于给定的随机变量,和期望值相差给定距离的取值发生的概率是多少?为了回答这个问题,本文将依次介绍马尔可夫不等式、切比雪夫不等式和切诺夫界。
1 马尔可夫不等式
1.1 结论
令 $Z$ 是非负的、整数随机变量,则
$$ \forall a \in \mathbb{R}^+: \Pr [Z \geq a] \leq \frac{\mathbb{E}[Z]}{a} $$
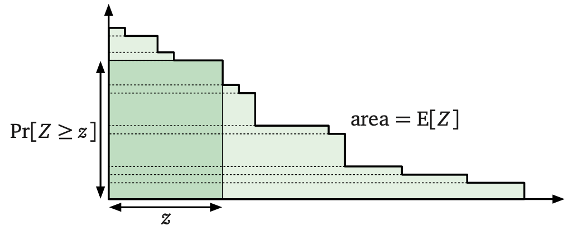
Proof #1:如图 1 所示,显然有 $z \cdot \Pr [Z \geq z] \leq \mathbb{E} [Z]$,变形可得结论。
Proof #2:因为 $\Pr [Z \geq a] = \int_a^\infty f(z) dz$ 且当 $z \geq a$ 时显然有 $\frac{z}{a} \geq 1$,故
$$ \Pr [Z \geq a] = \int_a^\infty f(z) dz \leq \int_a^\infty \frac{z}{a} f(z) dz $$ 此外,
$$ \frac{\mathbb{E}[Z]}{a} = \mathbb{E}\bigg[\frac{Z}{a}\bigg] = \int_0^\infty \frac{z}{a} f(z) dz = \int_0^a \frac{z}{a} f(z) dz + \int_a^\infty \frac{z}{a} f(z) dz \geq \int_a^\infty \frac{z}{a} f(z) dz $$ 联立两式可得结论。
1.2 推论
基于马尔科夫不等式,可以得到和期望相差一定距离的随机变量的取值发生的概率的上限:
$$ \Pr \Big[Z \geq (1 + \delta) \mathbb{E}[Z] \Big] \leq \frac{1}{1 + \delta} $$
2 切比雪夫不等式
2.1 形式 1
对于一组指示(随机)变量 $X_1, X_2, ..., X_n \in \{0,1\}$,令 $p_i = \mathbb{E} [X_i] = \Pr [X_i = 1]$。定义 $X = \sum_i X_i$,定义 $\mu = \mathbb{E}[X] = \sum_i p_i$。如果 $X_1, X_2, ..., X_n$ 成对独立,则
$$ \Pr \Big[(X - \mu)^2 \geq z\Big] < \frac{\mu}{z} $$
Proof:$\forall i$,定义 $Y_i = X_i - p_i$,定义 $Y = \sum_i Y_i = X - \mu$。则
$$ \begin{align} \mathbb{E} [Y^2] = \mathbb{E} \Big[\sum_{i,j} Y_i \cdot Y_j \Big] &= \sum_{i} \mathbb{E} [Y_i^2] + \sum_{i \neq j} \mathbb{E} [Y_i \cdot Y_j] \\ &= \sum_{i} \mathbb{E} [Y_i^2] + \sum_{i \neq j} \mathbb{E} [Y_i] \cdot \mathbb{E} [Y_j] && \textrm{成对独立} \\ &= \sum_{i} \mathbb{E} [Y_i^2] && \forall i, \mathbb{E} [Y_i] = 0 \end{align} $$
对 $\sum_{i} \mathbb{E} [Y_i^2]$ 展开可得:$\sum_i \mathbb{E} [Y_i^2] = \sum_{i} (1 - p_i)^2 \cdot p_i + (- p_i)^2 \cdot (1 - p_i) = \sum_i p_i (1 - p_i) < \sum_i p_i = \mu$。因此,可得 $\mathbb{E}[Y^2] < \mu$。
带入马尔可夫不等式可得
$$ \Pr [Y^2 \geq z] \leq \frac{\mathbb{E} [Y^2]}{z} < \frac{\mu}{z} $$
证毕。
2.2 推论 1
$\forall \Delta, \delta \in \mathbb{R}^+$,有
$$ \begin{aligned} \Pr \big[X \geq \mu + \Delta \big] < \frac{\mu}{\Delta^2} \qquad \Pr \big[X \geq (1 + \delta) \mu \big] < \frac{1}{\delta^2 \mu} \\ \Pr \big[X \leq \mu - \Delta \big] < \frac{\mu}{\Delta^2} \qquad \Pr \big[X \leq (1 - \delta) \mu \big] < \frac{1}{\delta^2 \mu} \end{aligned} $$
以上结论通过带入 $z = \Delta^2$、$\Delta = \delta \mu$ 到切比雪夫不等式来证明。
2.3 推论 2
将随机变量 $X_1, X_2, ..., X_n \in \{0,1\}$ 解读为 $n$ 次重复独立试验,即 $\Pr [X_i = 1] = p$,此时 $\mu = n p$。令 $\bar{X}_n = \frac{1}{n}\sum_{i=1}^n X_i$ 为前 $n$ 次重复独立试验的样本均值,则可以得到弱大数定理:
$$ \lim_{n \to \infty} \Pr \Big[|\bar{X}_n - p| \geq \epsilon \Big] = 0 $$
2.4 形式 2
对于随机变量 $X$,定义 $\mu = \mathbb{E} [X]$,$\sigma = \sqrt{\textrm{Var}(X)}$,则
$$ \Pr \Big[|X - \mu| \geq k \sigma \Big] \leq \frac{1}{k^2}, \quad k > 0 $$
Proof:定义 $Y = |X - \mu| > 0$,则由马尔可夫不等式可得 $\Pr [|X - \mu| \geq a] < \frac{\mathbb{E} [|X - \mu|]}{a}$,两边同时平方可得
$$ \Pr \Big[|X - \mu| \geq a \Big] \cdot \Pr \Big[|X - \mu| \geq a \Big] < \frac{\mathbb{E} \big[|X - \mu| \big] \cdot \mathbb{E} \big[|X - \mu| \big]}{a^2} $$
$X - \mu$ 的本质是样本的测量误差,每次测量都服从独立同分布(其实是正态分布),又因为对于给定的 $f(⋅)=|⋅|$ 仍然有 $|X-\mu|$ 服从独立同分布,所以 $\mathbb{E} \big[|X - \mu| \big] \cdot \mathbb{E} \big[ |X - \mu| \big] = \mathbb{E} \big[(X - \mu)^2 \big] = \sigma^2$(这里运用了随机变量的独立性)。
对于前后两次测量,事件 $\{\omega \in \Omega \mid |X(\omega) - \mu| \geq a \}$ 和 $\{ \omega \in \Omega \mid |X(\omega) - \mu| \geq a \}$ 独立,所以 $\Pr \big[|X - \mu| \geq a \big] \cdot \Pr \big[ |X - \mu| \geq a \big] = \Pr \big[ |X - \mu| \geq a \wedge |X - \mu| \geq a \big] = \Pr \big[| X - \mu| \geq a \big]$。所以
$$ \Pr \Big[|X - \mu| \geq a \Big] < \frac{\sigma^2}{a^2} $$
令 $a = \frac{k}{\sigma}$ 即可得到结论。证毕。
可以发现,切比雪夫不等式比马尔科夫不等式更加精确。
3 Higher Moment Inequalities
结论:切比雪夫不等式成立的条件是要求 $X_1,X_2,...,X_n$ 成对独立,即 2$k$-wise independent 且 $k=1$。如果 $X_1,X_2,...,X_n$ 满足 $2k$-wise independent,则
$$ \Pr \Big[(X - \mu)^k \geq z\Big] \leq \mathcal{O} \bigg(\frac{\mu^k}{z}\bigg) $$
其中 $\mathcal{O} (\cdot)$ 中的隐藏参数与 $k$ 有关。
推论:$\forall \Delta, \delta \in \mathbb{R}^+$,有
$$ \begin{aligned} \Pr \big[X \geq \mu + \Delta \big] = \mathcal{O} \Bigg( \bigg(\frac{\mu}{\Delta^2} \bigg)^k \Bigg) \qquad \Pr \big[X \geq (1 + \delta) \mu \big] = \mathcal{O} \Bigg( \bigg( \frac{1}{\delta^2 \mu} \bigg)^k \Bigg) \\ \Pr \big[X \leq \mu - \Delta \big] = \mathcal{O} \Bigg( \bigg(\frac{\mu}{\Delta^2} \bigg)^k \Bigg) \qquad \Pr \big[X \leq (1 - \delta) \mu \big] = \mathcal{O} \Bigg( \bigg( \frac{1}{\delta^2 \mu} \bigg)^k \Bigg) \end{aligned} $$
这个推论通过将 $z = \Delta^2$、$\Delta = \delta \mu$ 带入上面的结论得到。
4 切诺夫界
4.1 引理
如果一组随机指示变量 $X_1,X_2,...,X_n$ 相互独立,令 $X = \sum_i X_i$,$\mu = \mathbb{E} [X] = \sum_i p_i$,则
$$ \forall \alpha \geq 1, \quad \mathbb{E} [\alpha^X] \leq e^{(\alpha - 1) \mu} $$
Proof:显然 $\mathbb{E} [\alpha^{X_i}] = p_i \alpha + (1 - p_i) = (\alpha - 1) p_i + 1$,因为 $1 + t \leq e^t$ 恒成立,所以 $\mathbb{E} [\alpha^{X_i}] \leq e^{(\alpha - 1) p_i}$。根据随机变量 $X_1,X_2,...,X_n$ 相互独立的性质可以得到
$$ \mathbb{E} [\alpha^X] = \mathbb{E} \Big[\alpha^{\sum_i X_i} \Big] =\prod_i \mathbb{E} \big[\alpha^{X_i} \big] \leq e^{(\alpha - 1)\mu} $$
4.2 切尔诺夫界 - upper tail
如果随机变量 $X_1,X_2,...,X_n$ 相互独立,则
$$ \forall x \geq \mu, \quad \Pr [X \geq x] \leq e^{x - \mu} \bigg( \frac{\mu}{x} \bigg)^x $$
Proof:当固定住 $x$ 且满足 $\frac{x}{\mu} \geq 1$,函数 $f: t \to \big( \frac{x}{\mu} \big)^t$,所以 $\Pr [X \geq x] = \Pr [(\frac{x}{\mu})^X \geq (\frac{x}{\mu})^x]$。根据马尔可夫不等式有
$$ \Pr \bigg[(\frac{x}{\mu})^X \geq (\frac{x}{\mu})^x \bigg] \leq \frac{\mathbb{E} \big[(\frac{x}{\mu})^X \big]}{(\frac{x}{\mu})^x} $$
根据引理可得 $\mathbb{E} \big[(\frac{x}{\mu})^X \big] \leq e^{x - \mu}$,所以可得 $\Pr [X \geq x] \leq e^{x - \mu} \big( \frac{\mu}{x} \big)^x$。
4.3 切尔诺夫界 - lower tail
如果随机变量 $X_1,X_2,...,X_n$ 相互独立,则
$$ \forall x \leq \mu, \quad \Pr \big[ X \leq x \big] \leq e^{x - \mu} \bigg( \frac{\mu}{x} \bigg)^x $$
Proof:固定住 $x$ 且满足 $\frac{x}{\mu} \leq 1$,则 $\Pr [X \leq x] = \Pr \Big[(\frac{x}{\mu})^X \geq (\frac{x}{\mu})^x \Big]$。剩余部分的证明和上面一样。
4.4 推论 1
将 $\frac{\mu}{x}$ 替换为 $\alpha$ 则有
$$ \begin{aligned} \forall \alpha > 1: \quad \Pr \big[X \geq x \big] \leq \frac{e^{(\alpha - 1) \mu}}{\alpha^x} \\ \forall \alpha < 1: \quad \Pr \big[X \leq x \big] \leq \frac{e^{(\alpha - 1) \mu}}{\alpha^x} \end{aligned} $$
可验证上述二式在 $\alpha = \frac{\mu}{x}$ 时取等。
4.5 推论 2
$\forall \Delta, \delta \in \mathbb{R}^+$,有
$$ \begin{aligned} \Pr \big[X \geq \mu + \Delta \big] \leq e^\Delta \bigg( \frac{\mu}{\mu + \Delta} \bigg)^{\mu + \Delta} \qquad \Pr \big[X \geq (1 + \delta) \mu \big] \leq \bigg( \frac{e^\delta}{(1 + \delta)^{1 + \delta}} \bigg)^\mu \\ \Pr \big[X \leq \mu - \Delta \big] \leq e^{-\Delta} \bigg( \frac{\mu}{\mu - \Delta} \bigg)^{\mu - \Delta} \qquad \Pr \big[X \leq (1 - \delta) \mu \big] \leq \bigg( \frac{e^{-\delta}}{(1 - \delta)^{1 - \delta}} \bigg)^\mu \end{aligned} $$
分别令 $x = \mu + \Delta$、$x = \mu - \Delta$、$\Delta = \delta \mu$,带入推论 1 可得。
4.6 推论 3
进一步地,还有更为松散的上界:
$$ \begin{aligned} \Pr [X \geq (1 + \delta) \mu] \leq \exp \bigg(- \frac{\delta^2 \mu}{3} \bigg) \\ \Pr [X \leq (1 - \delta) \mu] \leq \exp \bigg(- \frac{\delta^2 \mu}{2} \bigg) \end{aligned} $$
Proof:将函数 $f(x) = \ln (x + 1)$,$x \geq -1$,在 $x = 0$ 处展开,得到
$$ f(x) \geq f(0) + f'(0) (x - 0) + \frac{f''(0)}{2} (x - 0)^2 $$
带入可得 $\ln (x + 1) \geq x - \frac{1}{2} x^2$。将 $x$ 替换为 $-\delta$ 并限定 $\delta \in [0,1]$ 得到 $\ln (1 - \delta) \geq - \delta + \frac{\delta^2}{2}$。代回推论 2 中右下方公式即可得本推论的公式 2。
此外,又因为 $\frac{1}{\ln (1 + x)} \leq \frac{1}{x (1 - \frac{1}{2} x)} = \frac{1}{x} + \frac{1}{2- x}$,将 $x$ 替换为 $\delta$ 并限定 $\delta \in [0,1]$ 可得 $\frac{1}{\delta} + \frac{1}{2 - \delta} \leq \frac{1}{\delta} + \frac{1}{2}$,所以可得 $\frac{1}{\ln (1 + \delta)} \leq \frac{1}{2} + \frac{1}{\delta}$。代回推论 2 中右上方公式即可得本推论的公式 1。
转载申请
本作品采用 知识共享署名 4.0 国际许可协议 进行许可,转载时请注明原文链接。您必须给出适当的署名,并标明是否对本文作了修改。