面向深度学习的互适应调度 · OSDI '21

所谓调度，需要回答的核心问题是：在何时将何种任务分配给何种资源以何种方式执行。 调度广泛存在于操作系统、编程语言运行时、容器编排和业务系统中， 其核心目的是“对有限的资源进行分配以实现最大化资源的利用率、降低系统的尾延迟或最小化任务的完工时间”。 关于调度系统的深入分析可以参见 调度系统设计精要。

本文将深入分析了一篇发表在 OSDI '21 上的论文 Pollux: Co-adaptive Cluster Scheduling for Goodput-Optimized Deep Learning。对于深度学习任务，该论文提出了一种同时考虑 “作业层级（per-job level）” 信息和 “集群层级（cluster-wide level）” 信息的调度策略，并将其命名为 Pollux。具体地，Pollux 通过观察每个作业的训练状态和集群的资源利用情况，周期性地作出如下两类决策：

1. 调整每个深度学习作业的批处理数据大小（batch size）和学习率（learning rate）；
2. 为每个深度学习作业重新分配集群资源（如 GPU）。

实验表明，和现有的深度学习调度器 Tiresias [OSDI '19]、Optimus [EruoSys '18] 相比，Pollux 可以将作业完成时间（job completion time，JCT）减少 37-50%。接下来，本文将从 Motivation、Background、Modeling 与 Architecture 分别进行阐述。

1 Motivation

深度学习模型的训练已经成为了云上最常见的一类工作负载。如何为这些深度学习模型的训练任务合理地分配昂贵的计算设备（如 GPU 和 TPU），使得任务尽可能早地被完成， 对于降低企业的成本而言大有裨益。现有的调度器通常需要任务的提交者手动配置该任务所需的资源配额， 例如，在 Kubernetes 中，可以在 yaml 中通过设定 spec.hard.memory 字段指定待创建的资源对象的内存配额 ¹。这意味着，资源的分配主要依赖于作业提交者的工程经验。 如果分配过多的 GPU 资源给某个任务，其他任务的等待时间将显著增加；如果分配过少，又会导致本任务的计算时间过长和资源闲置。 一个好的调度策略应当根据全体作业的运行状况和集群资源的利用率实时地作出调度决策。 除了资源配额，如何配置深度学习模型在训练时的批处理大小（batch size）和学习率（learning rate）也会显著影响训练时间。 然而，这两个参数的设定也主要依赖于工程师的经验。

一个正确配置的深度学习训练任务应当在以下两个指标之间取得平衡：

1. 系统吞吐量（system throughput）。在训练任务中，该指标可以用 “每个时钟周期处理的样本个数” 进行测算；
2. 工作效率（statistical efficiency）。该指标可以用 “每处理单个训练样本在模型参数上所取得的进展” 来衡量。

实际上，在这二者之间取得权衡是很困难的。如图 1 所示，通常情况下，如果分配给某个任务的资源越多，那么将该任务的 batch size 增大一些，显然可以提高系统吞吐量； 但是，工作效率却可能会因此显著下降。关于这一点，我们会在章节 2 给出分析。

Pollux 要做的，就是协同地进行 系统资源的分配（主要是 GPU） 和 任务参数的设定（主要是 batch size 和 learning rate），在维持系统吞吐量和工作效率之间的平衡的同时，尽可能早地完成任务。

2 Background

训练一个深度学习模型，在本质上是最小化一个损失函数： $$ \begin{equation} \mathcal{L} (w) = \frac{1}{|X|} \sum_{x_i \in X} l(w, x_i), \tag{e.q. 1} \end{equation} $$ 其中 $w \in \mathbb{R}^d$ 是模型参数，$X$ 是训练集，$x_i$ 是一个训练样本，$l$ 是定义在每一个训练样本上的损失函数。 通常采用随机梯度下降算法（Stochastic Gradient Descent，SGD）及其变种最小化 $\mathcal{L} (w)$ ²。 以 SGD 为例，每一轮迭代通过 $$ \begin{equation} w^{(t+1)} = w^{(t)} - \eta \hat{g}^{(t)} \tag{e.q. 2} \end{equation} $$ 更新参数 $w$，其中 $\eta$ 是学习率，$\hat{g}^{(t)}$ 是在某个随机小批量数据 $\mathcal{M}^{(t)}$ 上计算得到的梯度： $$ \begin{equation} \hat{g}^{(t)} = \frac{1}{M} \sum_{x_i \in \mathcal{M}^{(t)}} \nabla l(w^{(t)}, x_i), \tag{e.q. 3} \end{equation} $$ 其中 $M = |\mathcal{M}^{(t)}|$。我们主要关心参数 $\eta$ 和 $M$ 的设定。

2.1 系统吞吐量

深度学习模型的训练通常以分布式的方式进行。系统吞吐量主要由如下几个因素决定：

• 为每个作业分配的 GPU 数量；
• 分布式训练的模式和数据同步的方法；
• 批处理数据大小（batch size）。

默认情况下，在主流的深度学习框架中，模型的训练以 同步数据并行（synchronous data-parallelism） 的方式执行。 具体地，在第 $t$ 轮迭代中，$w^{(t)}$ 被复制到所有的、$K$ 个 GPU 的显存上，$\mathcal{M}^{(t)}$ 被随机均匀划分为 $K$ 份：$\mathcal{M}_1^{(t)},...,\mathcal{M}_K^{(t)}$。 每个 GPU 根据自己得到的数据计算局部梯度： $$ \begin{equation} \hat{g}^{(t)}_k = \frac{1}{m} \sum_{x_i \in \mathcal{M}_k^{(t)}} \nabla l(w^{(t)}, x_i), \qquad \forall k = 1, ..., K, \tag{e.q. 4} \end{equation} $$ 其中 $m = |\mathcal{M}_k^{(t)}|$。随后，将这些局部梯度进行平均化操作（averaging）得到全局梯度 $\hat{g}^{(t)}$ $$ \hat{g}^{(t)} = \frac{1}{K} \sum_{k} \hat{g}^{(t)}_k, $$ 并通过 $(\textrm{e.q. 2})$ 得到参数 $w^{(t+1)}$。然后进入下一轮迭代。

每一轮迭代的运行时间主要由两部分组成：其一是计算梯度 $\hat{g}^{(t)}_k$ 的时间，记为 $T_{grad}$；其二是平均化操作的时间 ³，记为 $T_{sync}$。 当分配的 GPU 增多时，如果不同时增大 batch size，$T_{grad}$ 会因为每个 GPU 分得的数据量变小了而减小， 但是 $T_{sync}$ 与 batch size 是独立的，并不会随之降低。相反地，$T_{sync}$ 会随着 GPU 的增多而变大。 这就会导致 $T_{sync}$ 成为瓶颈。当分配的 GPU 增多时，增大 batch size 对于提升系统吞吐量而言是一个妥善的决策。

2.2 工作效率

工作效率可以用 “梯度噪声比例（gradient nosie scale，GNS）” 来评估。GNS 描述了随机梯度中 “噪声和有效信号” 之间的比例。 如果噪声较大，那么适当增大 batch size 和 learning rate 可以 “相对” 减缓工作效率下降的趋势； 如果噪声较小，增大 batch size 和 learning rate 可能会显著降低工作效率。 工作效率的下降是不可避免的，其本质原因是边际效应的递减。Pollux 要做的，就是尽量减缓工作效率下降的速度。

此外，现有的研究成果表明，在增加 batch size 的时候，也应该同步增大 learning rate，否则模型的质量会打上折扣。 但是，以何种速度增大 learning rate 要视具体的模型和采取的优化算法而定。 常见的规则有 linear scaling rule（$\eta \propto M$）和 squart-root rule（$\eta \propto \sqrt{M}$）等。

2.3 现有工作

目前学术界和工业界主流的调度器可以分成两大类：尺度自适应的调度器（scale-adaptive）和非自适应的调度器（non-scale-adaptive）。

• 非自适应的调度器要求用户在提交作业时指定所需要的资源数量，且不会随着任务的状态调整资源的分配。例如，Tiresias [OSDI '19] 和 Gandiva [OSDI '18] 等。
• 自适应的调度器会主动调整资源分配。例如，Optimus [EruoSys '18] 训练了一个系统吞吐量关于各作业资源分配状态的预测模型，并根据这个模型调整资源的配比，从而最小化 JCT。此外还有 Gavel [OSDI '20]、AntMan [OSDI '20]、Themis [NSDI '20]，不一而足 ⁴。

和这些工作相比，Pollux 不仅给出了资源的动态分配方案，还 “将触手伸到了每个作业内部” 去调整这些模型训练本身的超参数：batch size 和 learning rate。 这就是 Pollux 可以取得更好的性能的直接原因。接下来将深入分析 Pollux 是如何对上述两个指标进行建模、如何调整资源的分配和作业的超参数的。

3 Modeling

3.1 Goodput 指标定义

综合系统吞吐量和工作效率这两个指标，Pollux 引入了 goodput 的概念：

定义（goodput）。一个深度学习模型的训练任务在第 $t$ 轮迭代的 goodput 是此时系统吞吐量和该任务在本轮迭代的工作效率的乘积： $$ \begin{equation} \texttt{GOODPUT}_t(\star) = \texttt{THROUGHPUT}(\star) \times \texttt{EFFICIENCY}_t(M(\star)), \tag{e.q. 5} \end{equation} $$ 其中 $\star$ 代表 “会对吞吐量和 batch size” 造成影响的三个参数，$\star = (a, m, s)$，其中：

• $a \in \mathbb{R}^N$：GPU 分配向量。$a_n$ 表示第 $n$ 个节点分配给本作业的 GPU 个数；
• $m \in \mathbb{Z}$：每轮迭代中每个 GPU 分得的批处理数据大小；
• $s \in \mathbb{Z}$：“梯度聚合” 操作的个数（gradient accumulation steps）⁵。

基于以上三者， $$ M(\star) = M(a, m, s) = \texttt{SUM}(a) \times m \times (s + 1). $$

一个作业被提交时需要指定 batch size $M_0$ 和学习率 $\eta_0$。当 Pollux 启动该作业时，会为其指定 单个 GPU，并按照如下方式初始化： $$ m = M = M_0, s = 0, \eta = \eta_0. $$ 在作业运行的同时，Pollux 会周期性地更新对 $\texttt{THROUGHPUT}$和 $\texttt{EFFICIENCY}$ 的预测模型（会在 $\S 3.2$ 和 $\S 3.3$ 给出模型的细节）， 并根据集群资源的状态和作业的训练情况更新 $(a, m, s)$。

如 $\S 2$ 所述，逐步增大 batch size 是合理的，且工作效率随着模型的训练逐步降低是不可避免的。 因此，在作业启动后，Pollux 总是逐步增大 batch size，即 $M \geq M_0$，且必然有 $$ \texttt{EFFICIENCY}_t(M) \leq \texttt{EFFICIENCY}_t(M_0). $$ 基于以上分析，我们可以将 goodput 解读为 “系统吞吐量中有效训练的那一部分的占比”。 在 $\S 2.2$ 中，我们还提到，在增加 batch size 的时候，也应该同步增大 learning rate。对此，Pollux 提供了一个通用的接口 $$ \texttt{SCALE_LR}(M_0,M) \to \lambda, $$ 基于 Pollux 的二次开发者提供自己对本函数的实现即可。该函数签名返回的 $\lambda$ 用于更新 learning rate：$\eta \leftarrow \lambda \eta$。

3.2 工作效率预测模型

本质上，$\texttt{EFFICIENCY}_t(M)$ 是 相对于使用 $M_0$，使用 $M$ 作为批处理数据大小时，单个训练样本所取得的进展。 如果训练算法是 SGD，那么 $\texttt{EFFICIENCY}_t(M)$ 可以直接用 GNS 来建模，即 $\frac{\textrm{tr}(\Sigma)}{\| g \|^2}$。 其中 $g$ 是真实梯度，$\Sigma$ 是通过各个样本得到的随机梯度的协方差 ⁶。 为了支持 Adam 和 AdaGrad 等改进的 SGD 算法，Pollux 用 pre-conditioned GNS（PGNS）⁷ 来建模： $$ \begin{equation} \varphi_t = \frac{\textrm{tr}(P \Sigma P^\mathrm{T})}{|P g|^2}, \tag{e.q. 6} \end{equation} $$ 其中 $P$ 是预处理矩阵。PGNS 是对 GNS 的一种泛化。

基于 $\varphi_t$，Pollux 将 $\texttt{EFFICIENCY}_t(M)$ 定义为 $$ \begin{equation} \texttt{EFFICIENCY}_t(M) = \frac{\varphi_t + M_0}{\varphi_t + M} \in (0, 1]. \tag{e.q. 7} \end{equation} $$ 若 $\texttt{EFFICIENCY}_t(M) = E$，则 $M \approx \frac{1}{E} M_0$， 即若想取得和 “使用 $M_0$ 作为批处理数据大小的训练任务” 一样的工作效率，至少得处理 $1/E$ 倍的训练样本。

在训练任务执行的同时，Pollux 会周期性地计算不同的 $M$ 下的 $\texttt{EFFICIENCY}_t(M)$ 来调整 batch size。

模型验证。观察图 2 可以发现，该预测模型可以很好地描述工作效率。

3.3 系统吞吐量预测模型

吞吐量是指 单位时间内处理的样本个数。Pollux 将每轮训练的吞吐量定义如下： $$ \begin{equation} \texttt{THROUGHPUT}(a, m, s) = \frac{M(a, m, s)}{T_{iter}(a, m, s)}, \tag{e.q. 8} \end{equation} $$ 其中 $T_{iter}(a, m, s)$ 是每轮训练所花的时间。$T_{iter}(a, m, s)$ 主要由 $T_{grad}$ 和 $T_{sync}$ 组成。

• $T_{grad}$ 主要取决于 “单个样本梯度反向传播所花费的时间” 以及“样本的个数”，因此 Pollux 将其建模为 $$ \begin{equation} T_{grad}(m) = \alpha_{grad} + \beta_{grad} \cdot m, \tag{e.q. 9} \end{equation} $$ 其中 $\alpha_{grad}$ 和 $\beta_{grad}$ 是预测模型的参数。
• $T_{sync}$ 是单次 averaging 的时间开销，主要取决于参与训练的 GPU 个数以及这些 GPU 所在的节点。显然，inter-node communication overhead 要高于 intra-node communication overhead。为了描述这一现象，令 $K = \texttt{SUM}(a)$，Pollux 将 $T_{sync}$ 建模为 $$ \begin{equation} \begin{aligned} T_{sync}(a, m) = \left\{ \begin{array}{ll} 0 & K = 1 \\\\ \alpha_{sync}^{local} + \beta_{sync}^{local} \cdot (K - 2) & N = 1, K \geq 2 \\\\ \alpha_{sync}^{node} + \beta_{sync}^{node} \cdot (K - 2) & \textrm{otherwise}. \end{array} \right. \end{aligned} \tag{e.q. 10} \end{equation} $$

现代深度学习框架在一定程度上允许 $T_{grad}$ 和 $T_{sync}$ 重合。 例如，三个 GPU 中有两个 GPU 已经完成了局部梯度的计算，那么在第三个 GPU 计算自身的局部梯度的同时，这两个 GPU 可以先进行 averaging。为了建模这一点，Pollux 令 $$ \begin{equation} T_{tier}(a, m, 0) = \bigg( T_{grad}(m)^\gamma + T_{sync}(a, m)^\gamma \bigg)^{\frac{1}{\gamma}}, \tag{e.q. 11} \end{equation} $$ 其中 $\gamma \geq 1$ 是预测模型的参数。显然，当 $\gamma = 1$ 时，$T_{tier} = T_{grad} + T_{sync}$； 当 $\gamma \to \infty$ 时，$T_{tier} = \max \{ T_{grad}, T_{sync} \}$。

在模型训练时，GPU 的内存可能会限制批处理数据大小 $m$ 的增长。换句话说，随着 batch size 的增加，GPU 可能无法再将全部的 $m$ 个样本 同时 加载至 GPU 显存进行梯度的计算。 一个好的解决方法是使用 梯度聚合技术 ，即将 per-GPU data batch 再切分成 $s$ 个小份，每次只加载 $\frac{m}{s}$ 个样本到显存计算梯度， 将这些梯度进行累加得到 $\sum_{x_i \in \mathcal{M}_k^{(t)}} \nabla l(w^{(t)}, x_i)$。 综上所述，

$$ \begin{equation} T_{iter}(a, m, s) = s \times T_{grad} (m) + \bigg( T_{grad}(m)^\gamma + T_{sync}(a, m)^\gamma \bigg)^{\frac{1}{\gamma}}. \tag{e.q. 12} \end{equation} $$

至此，$\texttt{THROUGHPUT}(a, m, s)$ 的预测模型已经讲解完毕。

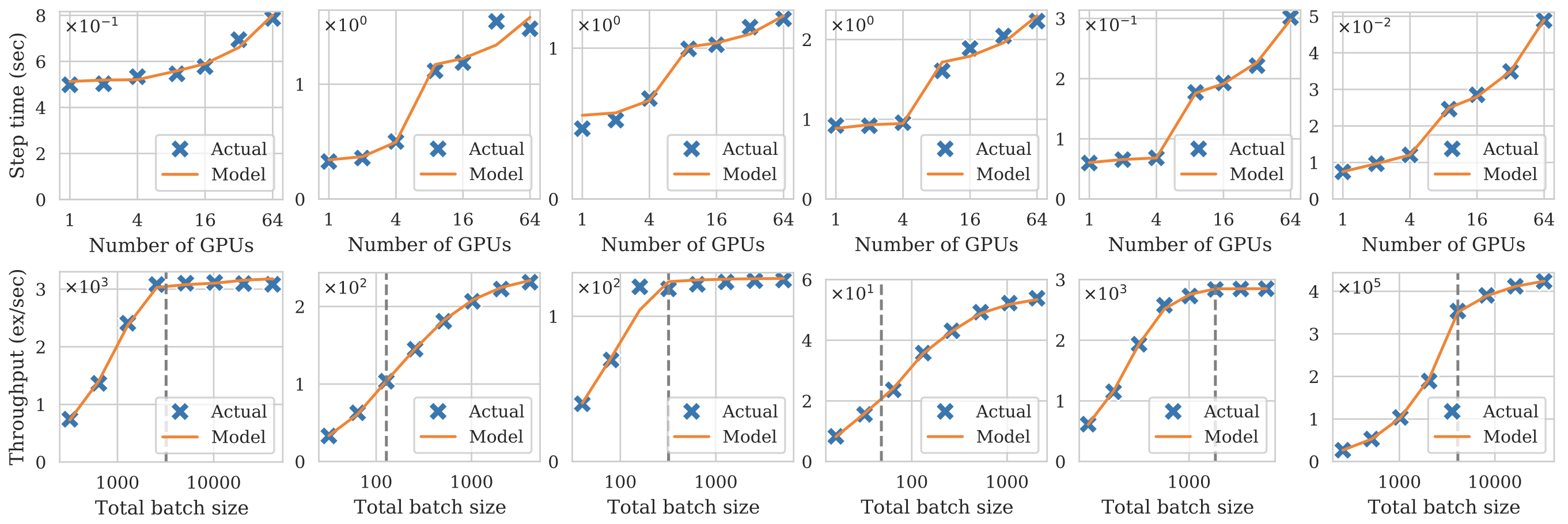
模型验证。吞吐量 $\texttt{THROUGHPUT}(a, m, s)$ 是很容易测算的。Pollux 作者基于 PyTorch、NCCL 对多个常见的深度学习模型在各种 $(a, m, s)$ 的参数设定下进行实验，发现该预测模型可以很好地描述系统的吞吐量。具体结果如图 3 所示。

4 Architecture

Pollux 需要在两个层面作出决策。在作业层面，Pollux 需要根据工作效率模型动态地选择最合适的 batch size，进而根据采取的规则更新 learning rate；在系统层面，Pollux 需要根据 goodput 动态地调整每个作业分得的 GPU 数量。Pollux 需要兼顾调度的公平性和 JCT。这两个层面的决策相互影响、相互妥协。这也是作者称其为 co-adaptive 的原因。

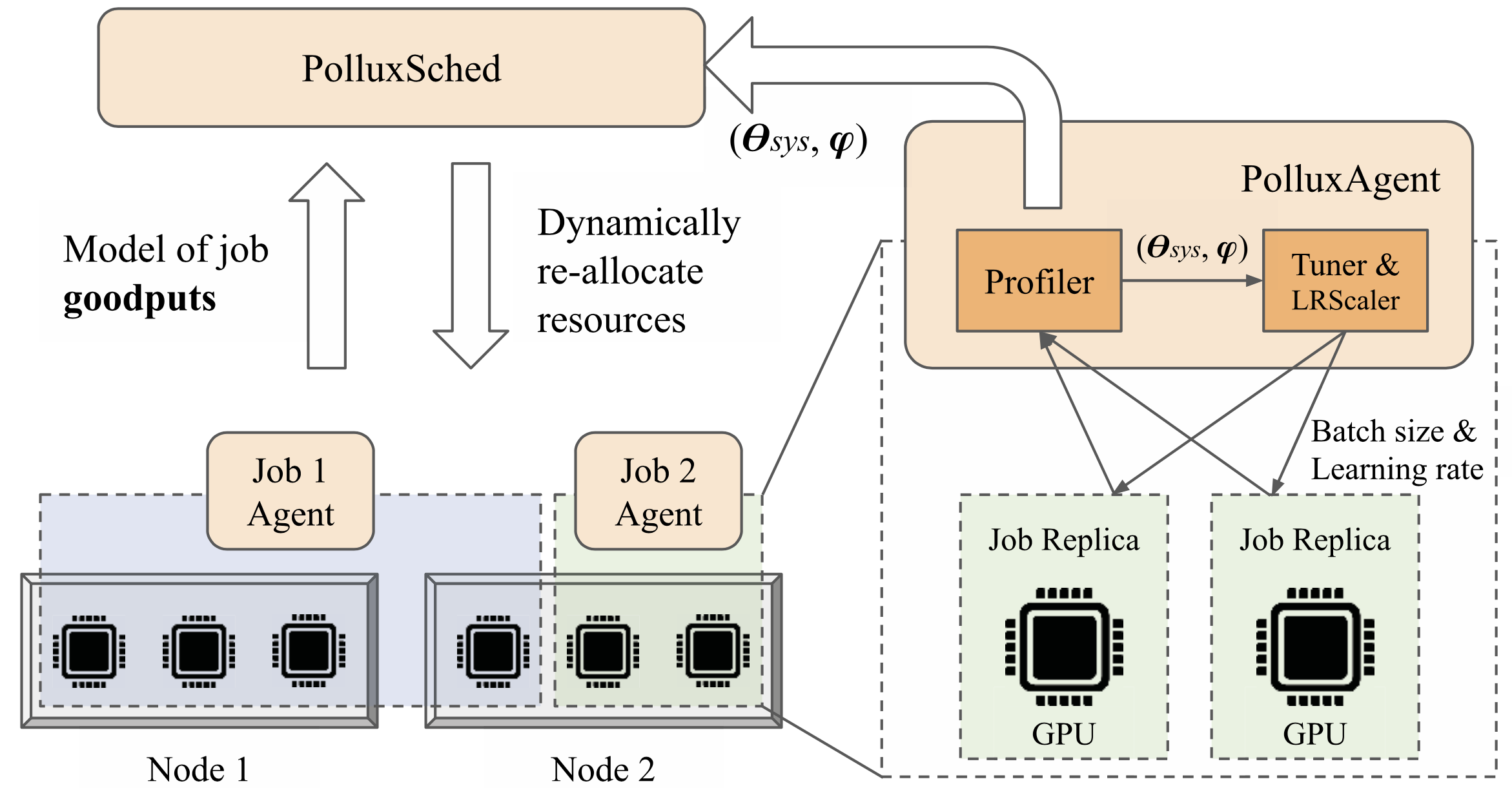
Pollux 的架构如图 4 所示。首先，每个作业都有一个对应的 PolluxAgent，该 agent 为与其绑定的作业运行着 $\texttt{THROUGHPUT}$ 和 $\texttt{EFFICIENCY}_t$ 预测模型（这两个模型在任务运行时在线拟合），并负责调整该作业的 batch size 和 learning rate。此外，PolluxAgent 定期向 PolluxSched 汇报本作业的 goodput 预测值。 PolluxSched 根据收集到的各个作业的 goodput 以及当前集群内 GPU 资源的竞争情况对所有运行着的作业 定期 进行资源的重新调度。PolluxSched 的调度决策还考量了资源分配的公平性等因素。

4.1 PolluxAgent：作业层级的优化

在线拟合预测模型。$\texttt{THROUGHPUT}$ 预测模型涉及以下 7 个参数： $$ \begin{equation} \theta_{sys} = \bigg( \alpha_{grad}, \beta_{grad}, \alpha_{sync}^{local}, \beta_{sync}^{local}, \alpha_{sync}^{node}, \beta_{sync}^{node}, \gamma \bigg), \tag{e.q. 13} \end{equation} $$ 而 $\texttt{GOODPUT}$ 的参数则可以用三元组 $(\theta_{sys}, \varphi_t, M_0)$ 描述。在 PolluxAgent 的生命周期中（从对应的作业的提交到结束被销毁），它会记录绑定的作业所有经历过的四元组 $(a, m, s, T_{iter})$，并定期地对参数 $\theta_{sys}$ 进行拟合。具体地，优化目标是 $(\textrm{e.q. 12})$ 和测算的真实值 $T_{iter}$ 之间的均方误差， 采用的优化算法是 L-BFGS-B ⁸。PolluxAgent 限定参数 $\alpha$ 和 $\beta$ 为非负数，$\gamma \in [1, 10]$。

初始化模型参数。$\theta_{sys}$ 的初值设定很重要。此时因为尚未开始对参数进行优化，如果盲目配置 $\theta_{sys}$，可能会导致调度的结果往错误的方向发展。 PolluxAgent 按如下方式进行设定：

• 如果一个作业尚未被分配多个 GPU，那么将 $\alpha_{sync}^{local}$ 置为 0；
• 如果一个作业的全部 GPU 均来自同一个节点，那么 $\alpha_{sync}^{local} = \beta_{sync}^{local}=0$；
• 如果一个作业被分配的 GPU 数量不超过两个，那么 $\beta_{sync}^{local}=\beta_{sync}^{node}=0$。

通过这样的设定，在作业刚起步的这段时间，PolluxSched 会 “乐意” 为该作业分配更多的 GPU 和更多的节点。此外，PolluxAgent 还对本作业所能分得的 GPU 数量的上限做了一个限制：不得超过在其生命周期内所获得的最大 GPU 数量的两倍。

更新作业超参数。有了 $\theta_{sys}$、$\varphi_t$ 和 $M_0$ 以及从 PolluxSched 获得的调度决策 $A$（$\S 4.2$）之后，PolluxAgent 按照如下方式选择对本作业而言当前最优的 batch size 和梯度聚合次数 $s$： $$ \begin{equation} (m^*, s^*) = \operatorname{argmax}_{m, s} \texttt{GOODPUT}(a, m , s). \tag{e.q. 14} \end{equation} $$ $(m^*, s^*)$ 是这样获得的：Pollux 会提供数个 $m$ 的候选，然后按照如下方式为每一个 $m$ 设定对应的 $s$： $$ s = \operatorname{argmin}_{s'} \bigg\{ \bigg \lceil \frac{M}{s'} \bigg \rceil \leq \textrm{GPU's memory size} \bigg\}. $$ 最后 Pollux 选择的是让 $\texttt{GOODPUT}(a, m , s)$ 最大的 $m$ 和 $s$。

基于 $m^*$，PolluxAgent 会调用相应的规则更新 learning rate。

4.2 PolluxSched：集群层级的优化

PolluxSched 周期性地为每个作业分配（重新分配）资源。 在每一个调度周期，PolluxSched 通过最大化如下目标获得调度决策 $A \in \mathbb{R}^{J \times N}$： $$ \begin{equation} \texttt{FITNESS}_p (A) = \bigg( \frac{1}{J} \sum_{j=1}^J \texttt{SPEEDUP}_j (A_j)^p \bigg)^{\frac{1}{p}}, \tag{e.q. 15} \end{equation} $$ 其中 $A_j \in \mathbb{R}^N$ 是作业 $j$ 的分配向量（即 $a$），$\texttt{SPEEDUP}_j$ 的定义如下： $$ \begin{equation} \texttt{SPEEDUP}_j (A_j) = \frac{\max_{m, s} \texttt{GOODPUT}_j (A_j, m, s)}{\max_{m, s} \texttt{GOODPUT}_j (a_f, m, s)}, \tag{e.q. 16} \end{equation} $$ 是相对于均匀分配策略（equal share）所取得的加速。在 $(\textrm{e.q. 16})$ 中，$a_f$ 是均匀分配向量，即每个作业都分得整个集群的 $\frac{1}{J}$ 比例的资源。 需要注意的是，$J$ 是在当前调度周期，系统中处于 running 和 pending 状态的作业的总数 ⁹。在 $\texttt{FITNESS}_p (A)$ 中，$p$ 是 fairness 参数：

• 当 $p = 1$ 时，$\texttt{FITNESS}_p (A)$ 衡量的是全体作业取得的 speedup 的均值；
• 当 $p \to - \infty$ 时，$\texttt{FITNESS}_p (A)$ 重点关注的是集群中取得 speedup 最小的作业。

Pollux 使用 遗传算法 最大化 $(\textrm{e.q. 15})$。

重新分配的惩罚。如果一个作业被决定调度到别的节点上继续执行，那意味着该作业需要保存当前进度到 checkpoint 中， Pollux 会杀死封装了该作业的 Pod，然后在新的节点上重新启动该作业。这必然会带来一定程度的延迟。 作者发现，基于 checkpoint-restart method，大约会产生 15～120 秒左右的延迟。 为了防止一个作业被反复重新分配到不同节点上，PolluxSched 为每个作业 $j$ 的 $\texttt{SPEEDUP}_j (A_j)$ 函数值乘上了一个重新分配的影响参数 $\texttt{REALLOC_FACTOR}$： $$ \texttt{SPEEDUP}_j (A_j) \leftarrow \texttt{SPEEDUP}_j (A_j) \times \texttt{REALLOC_FACTOR}_j(\delta). $$ 其中 $$ \texttt{REALLOC_FACTOR}_j(\delta) = \frac{T_j - R_j \delta}{T_j + \delta}, $$ $T_j$ 是该作业的存在时间，$R_j$ 是到目前为止为该作业重新分配资源的次数，$\delta$ 是对本作业重新分配时常的估计。

其他。为了尽可能减少不同作业在同一个节点上由于梯度同步所造成的网络干扰（interference），Pollux 限定每个节点上最多只运行一个作业 ¹⁰。此外，如果作业的提交者不希望 batch size 被 Pollux 修改，可以在提交作业的时候指定 batch size 为固定值 $M_0$。

最后

Pollux 在一个拥有 16 个节点（AWS EC2 g4dn.12xlarge）、单个节点拥有 4 台 NVIDIA T4 GPU、48 个 vCPU、192GB 内存、900GB SSD 的集群上做实验。 通过和 Tiresias 及 Optimus 进行对比，可以发现，即使为这两个调度器上运行的作业提供了 fine-tuned 超参数，Pollux 依然可以将 JCT 缩短 20~33%。

和现有的调度器相比，Pollux 最大的创新是，深入到作业内部去修改作业的超参数，这大大增加了调度的灵活性。

本文所有图片来自 Pollux 论文原文。

转载申请

本作品采用 知识共享署名 4.0 国际许可协议 进行许可，转载时请注明原文链接。您必须给出适当的署名，并标明是否对本文作了修改。