优化算法的目标函数通常是一个基于训练数据集的损失函数,优化的目标在于降低训练误差。 而深度学习的目标在于降低泛化误差。为了降低泛化误差, 除了使用优化算法降低训练误差以外,还需要注意应对过拟合。在接下来的内容中,我们只关注优化算法在最小化目标函数上的表现,而不关注模型的泛化误差。
深度学习中绝大多数目标函数都很复杂。因此,很多优化问题并不存在解析解,而需要使用基于数值方法的优化算法找到近似解,即数值解。为了求得最小化目标函数的数值解, 我们将通过优化算法有限次迭代模型参数来尽可能降低损失函数的值。
其中的两大挑战是 局部最小值 和 鞍点。
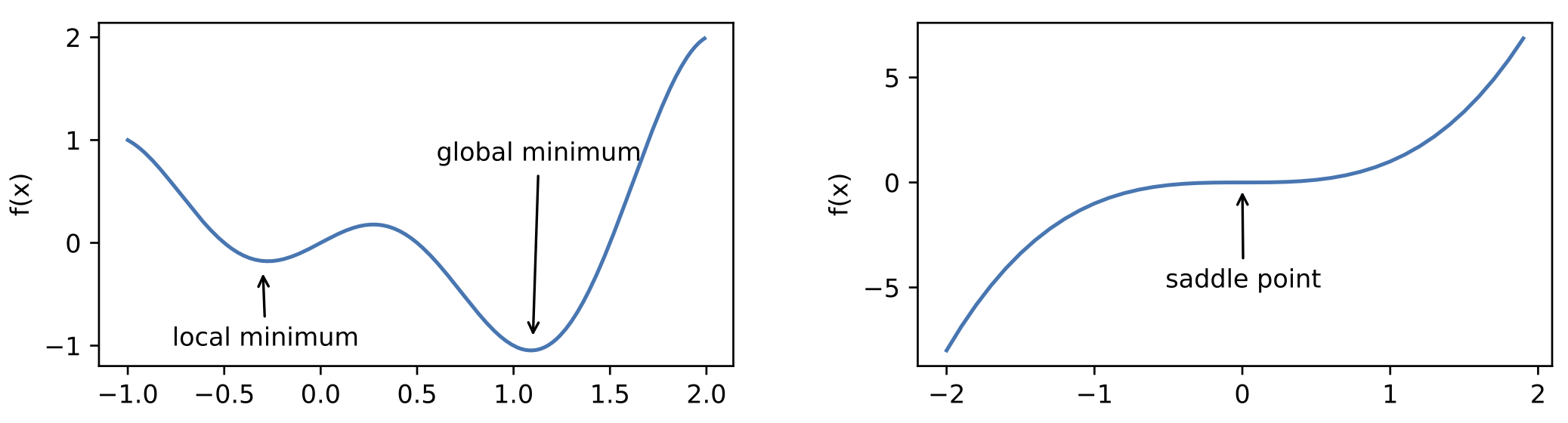
图 2 给出了三维空间中的鞍点示例。在该示例中,目标函数在 $x$ 轴方向上是局部最小值,但在 $y$ 轴方向上是局部最大值。
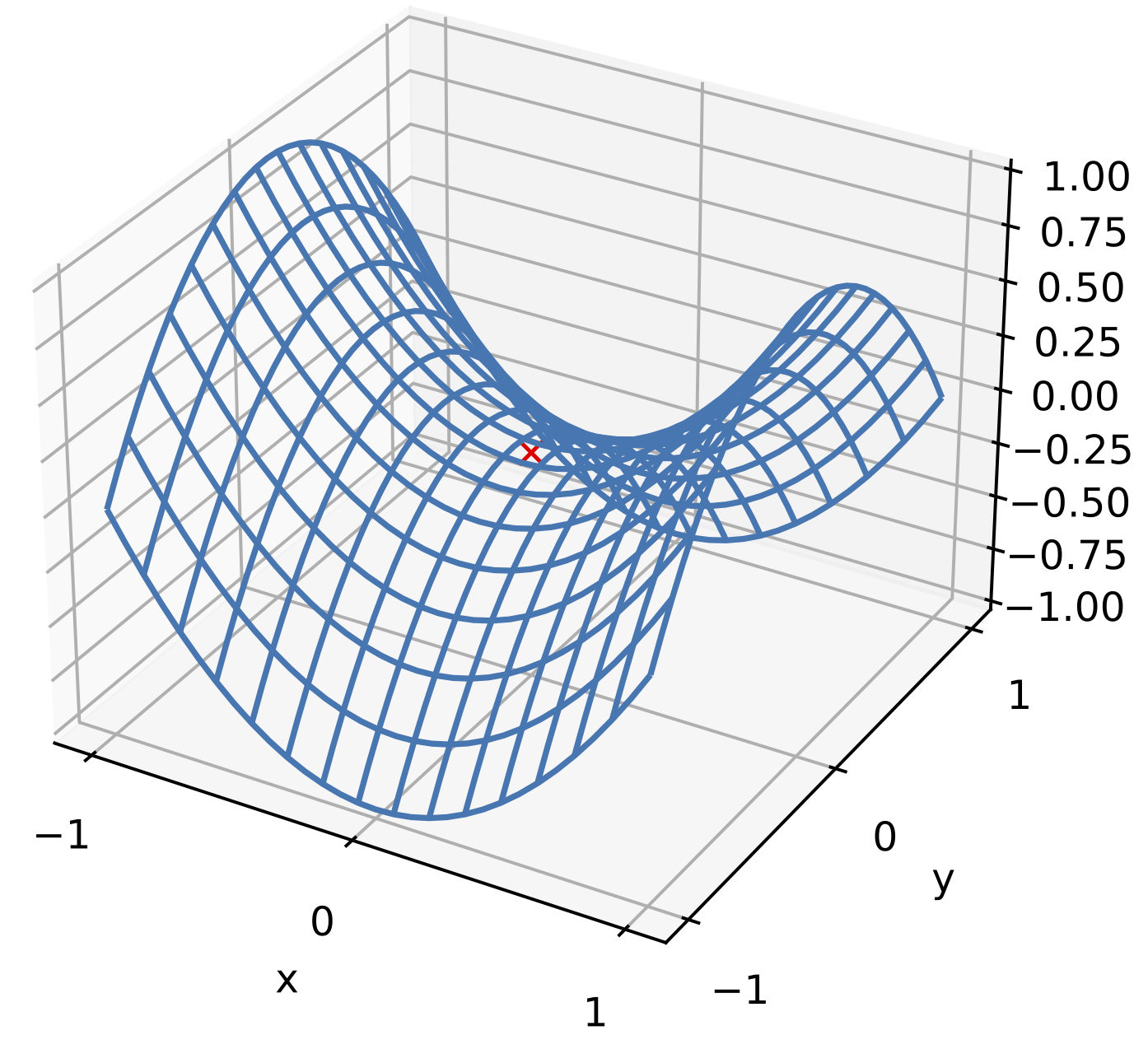
假设一个函数的输入为 $k$ 维向量,输出为标量,那么它的海森矩阵(Hessian matrix)有 $k$ 个特征值。该函数在梯度为 $0$ 的位置上可能是局部最小值、局部最大值或者鞍点。
- 当函数的海森矩阵在梯度为零的位置上的特征值全为正时,该函数得到局部最小值;
- 当函数的海森矩阵在梯度为零的位置上的特征值全为负时,该函数得到局部最大值;
- 当函数的海森矩阵在梯度为零的位置上的特征值有正有负时,该函数得到鞍点。
随机矩阵理论表明,对于一个大的高斯随机矩阵来说,任一特征值是正或者是负的概率都是 0.5。由于深度学习模型参数通常都是高维的, 所以目标函数的鞍点通常比局部最小值更常见。
接下来将依次介绍梯度下降系列算法以及在其上的各种改进方法。
梯度下降方法
虽然梯度下降(gradient descent)在深度学习中很少被直接使用,但理解梯度的意义以及沿着梯度反方向更新自变量可能降低目标函数值的原因是学习后续优化算法的基础。随后, 我们将引出随机梯度下降(stochastic gradient descent)和小批量梯度下降(mini-batch gradient descent)。
一维梯度下降
设函数 $f: \mathbb{R} \rightarrow \mathbb{R}$ 是一个连续可导的函数,将其在 $x$ 处泰勒展开:
$$ f(x + \epsilon) \approx f(x) + \epsilon f'(x), $$
其中 $\epsilon$ 是一个很小的数。选取 $\epsilon = -| \eta f'(x) |$,其中 $\eta$ 是一个很小的正常数,则
$$ f \big(x - \eta f'(x) \big) \approx f(x) - \eta f'(x)^2. $$
若 $f'(x) \neq 0$,则
$$ f \big(x - \eta f'(x) \big) \lesssim f(x), $$
这意味着可以通过
$$ x \leftarrow x - \eta f'(x) $$
来迭代 $x$,从而使得函数值降低。
多维梯度下降
设 $f: \mathbb{R}^d \rightarrow \mathbb{R}$ 是一个连续可导的函数,则任意点 $\vec{x}$ 上的梯度为
$$ \nabla f(\vec{x}) = \Big[ \frac{\partial f(\vec{x})}{\partial x_1}, ..., \frac{\partial f(\vec{x})}{\partial x_d} \Big]^\textrm{T} \in \mathbb{R}^{d}. $$
梯度中每个偏导数 $\frac{\partial f(\vec{x})}{\partial x_i}$ 代表 $f$ 在 $\vec{x}$ 有关输入 $x_i$ 的变化率。定义 $f$ 在 $\vec{x}$ 沿着单位方向 $\vec{u}$ 的方向导数为
$$ D_{\vec{u}} f(\vec{x}) \triangleq \lim_{h \to 0} \frac{f(\vec{x} + h \vec{u}) - f(\vec{x})}{h} = \nabla f(\vec{x}) \cdot \vec{u} = \Vert \nabla f(\vec{x}) \Vert \cdot \cos(\theta), $$
其中 $\theta$ 为梯度和 $\vec{u}$ 之间的夹角。
方向导数 $D_{\vec{u}} f(\vec{x})$ 给出了 $f$ 在 $\vec{x}$ 上沿着所有可能方向的变量率。当 $\theta = \pi$,即 $\vec{u}$ 在梯度方向的反方向时,
方向导数 $D_{\vec{u}} f(\vec{x})$ 区最小值,这就是 $f$ 被降低最快的方向。这意味着可以通过
$$ \vec{x} \leftarrow \vec{x} - \eta \nabla f(\vec{x}) $$
来迭代 $\vec{x}$,其中 $\eta$ 是人为添加的学习率。
随机梯度下降
设 $f_i(\vec{x})$ 是有关索引为 $i$ 的训练数据样本的损失函数,$n$ 是训练数据样本数,$\vec{x}$ 是模型的参数向量,那么目标函数定义为
$$ f (\vec{x}) = \frac{1}{n} \sum_{i=1}^n f_i(\vec{x}), $$
目标在 $\vec{x}$ 处的梯度计算为
$$ \nabla f (\vec{x}) = \frac{1}{n} \sum_{i=1}^n \nabla f_i(\vec{x}). $$
在随机梯度下降中,每一轮迭代随机采样一个样本索引 $i$ 来更新模型参数 $\vec{x}$:
$$ \vec{x} \leftarrow \vec{x} - \eta \nabla f_i(\vec{x}). $$
因为 $\mathbb{E} \big[\nabla f_i(\vec{x})\big] \approx \frac{1}{n} \sum_{i=1}^n \nabla f_i(\vec{x}) = \nabla f (\vec{x})$,
所以随机梯度是对梯度的 无偏估计。
小批量梯度下降
在每一次迭代中,梯度下降使用整个训练数据集来计算梯度,因此它有时也被称为批量梯度下降(batch gradient descent)。 如无特别说明,本章节后文的梯度下降均指批量梯度下降。而随机梯度下降在每次迭代中只随机采样一个样本来计算梯度。 我们还可以在每轮迭代中随机均匀采样多个样本来组成一个小批量,然后使用这个小批量来计算梯度,这就是小批量梯度下降。
设目标函数 $f(\vec{x}): \mathbb{R}^d \to \mathbb{R}$,其中 $\vec{x}$ 为待学习的参数。在迭代开始前的时间步设为 0。该时间步的自变量记为 $\vec{x}_0$,
通常由随机初始化得到。在接下来的每一个时间步 $t > 0$ 中,小批量随机梯度下降随机均匀采样一个由训练数据样本索引组成的小批量 $\mathcal{B}_t$。
我们可以通过重复采样(sampling with replacement)或者不重复采样(sampling without replacement)得到一个小批量中的各个样本。
前者允许同一个小批量中出现重复的样本,后者则不允许如此,且更常见。对于这两者间的任一种方式,都可以使用
$$ \vec{g}_t \leftarrow \nabla f_{\mathcal{B}_t} (\vec{x}_{t-1}) = \frac{1}{|\mathcal{B}_t|} \sum_{i \in \mathcal{B}_t} \nabla f_i (\vec{x}_{t-1}) $$
来计算时间步 $t$ 的小批量 $\mathcal{B}_t$ 上目标函数位于 $\vec{x}_{t-1}$ 处的梯度 $\vec{g}_t$。这里 $\mathcal{B}_t$ 代表小批量中样本的个数,
是一个超参数。$\vec{g}_t$ 是对 $\nabla f (\vec{x}_{t-1})$ 的无偏估计。给定学习率 $\eta_t > 0$,小批量随机梯度下降对自变量的迭代如下:
$$ \vec{x}_t \leftarrow \vec{x}_{t-1} - \eta_t \vec{g}_t. $$
为什么小批量梯度下降需要衰减学习率?
因为基于随机采样得到的梯度的方差在迭代过程中无法减小,在逼近局部极小值点时不可避免会震荡。相比之下,梯度下降则不需要衰减学习率。
这是因为梯度下降中的 $\vec{g}_t$ 就是目标函数的真实梯度,而非无偏估计的结果。
动量法
目标函数有关自变量的梯度代表了目标函数在自变量当前位置下降最快的方向。因此,梯度下降也叫作最陡下降(steepest descent)。在每次迭代中,梯度下降根据自变量当前位置, 沿着当前位置的梯度更新自变量。然而,如果自变量的迭代方向仅仅取决于自变量当前位置,如图 3 所示,会带来一些问题。
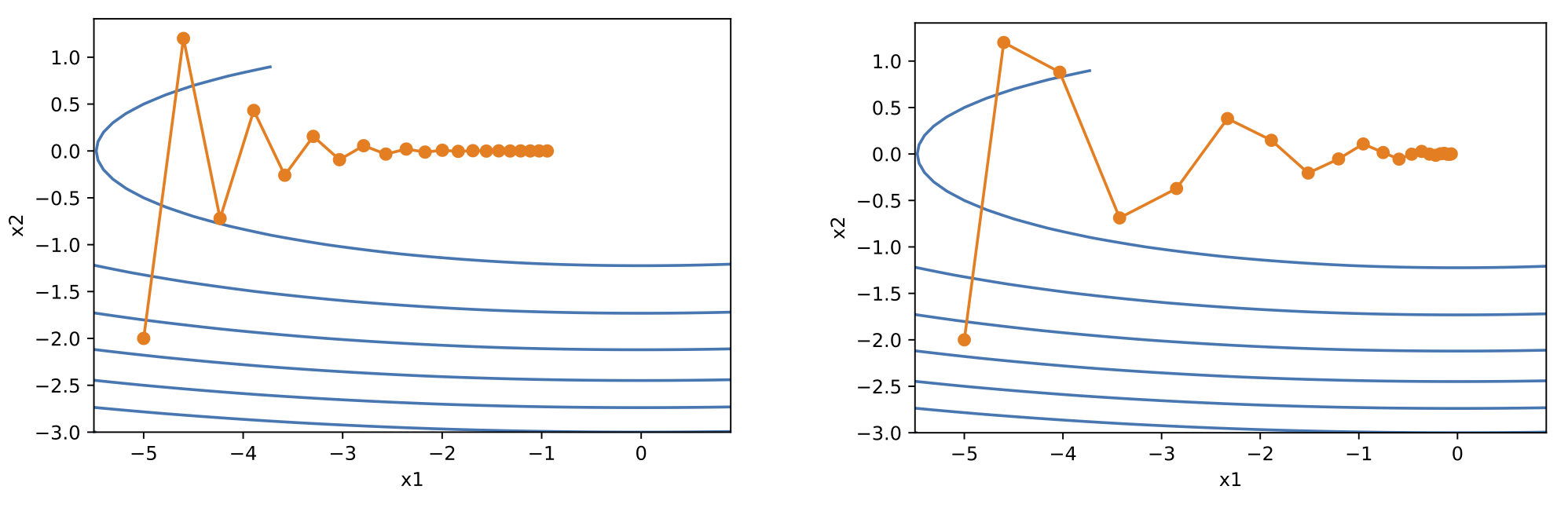
引入动量法可解决这一问题。设 $\vec{g}_t$ 表示时间步 $t$ 的小批量随机梯度,引入速度 $\vec{v}_t$,将模型参数 $\vec{x}_t$ 按照如下方式更新:
$$ \begin{aligned} \vec{v}_t &\leftarrow \gamma \vec{v}_{t-1} + \eta_t \vec{g}_t \\ \vec{x}_t &\leftarrow \vec{x}_{t-1} - \vec{v}_t, \end{aligned} $$
其中 $\gamma \in [0, 1)$,$\vec{v}_0$ 初始化为 $\vec{0}$。
接下来借助指数加权移动平均的概念来解释动量法的数学原理。
指数加权移动平均
给定超参数 $\gamma \in [0, 1)$,当前时间步 $t$ 的变量 $y_t$ 是上一时间步 $t-1$ 的变量 $y_{t-1}$ 和当前时间步的另一变量 $x_t$ 的线性组合:
$$ y_t = \gamma y_{t-1} + (1 - \gamma) x_t, $$
对 $y_t$ 按时间步展开:
$$ \begin{aligned} y_t &= (1 - \gamma) x_t + \gamma y_{t-1} \\ &= (1-\gamma) \Big( x_t + \gamma x_{t-1} + \gamma^2 x_{t-2} \Big) + \gamma^3 y_{t-3} \\ &= \cdots \end{aligned} $$
我们想忽略更高阶的项,因此需要分析 $\gamma$ 的指数 $n$。为了和自然对数 $e$ 建立关联,令 $n = \frac{1}{1 - \gamma}$,则 $\gamma = 1 - \frac{1}{n}$,且
$$ \lim_{\gamma \to 1} \gamma^n = \lim_{\gamma \to 1} \gamma^{1/(1-\gamma)} = \lim_{n \to \infty} \Big( 1 - \frac{1}{n} \Big)^n = \exp(-1) \approx 0.3679. $$
我们将 $\exp(-1)$(即 $\lim_{\gamma \to 1} \gamma^{1/(1-\gamma)}$ 的近似)视为一个比较小的数,
并忽略包含 $\lim_{\gamma \to 1} \gamma^{1/(1-\gamma)}$ 在内的高阶小量,那么,以 $\gamma = 0.95$ 为例,$y_t$ 近似为
$$ y_t \approx 0.05 \sum_{i=0}^{19} 0.95^i x_{t-i} = \frac{\sum_{i=0}^{19} 0.95^i x_{t-i}}{20}. $$
因此,我们常常将 $y_t$ 看作是对最近 $\frac{1}{1 - \gamma}$ 个时间步的 $x_t$ 值的加权平均,距离当前时间步越近权重越大。
理解动量法
在动量法中,速度 $\vec{v}_t$ 的更新可改写为:
$$ \vec{v}_t \leftarrow \gamma \vec{v}_{t-1} (1 - \gamma) \Big( \frac{\eta_t}{1-\gamma} \Big). $$
这实际上是对序列 $$\{\frac{\eta_{t-i}}{(1-\gamma)} \vec{g}_{t-i}: i=0, ..., \frac{1}{1-\gamma} -1 \}$$ 做了指数加权移动平均。动量法在每个时间步的自变量更新量近似于将最近 $\frac{1}{1-\gamma}$ 个时间步的普通更新量(即学习率乘以梯度)做了指数加权移动平均后再除以 $1-\gamma$(因为又除以了 $1-\gamma$,所以其实是加权和)。这意味着 自变量在各个方向上的移动幅度不仅取决当前梯度,还取决于过去的各个梯度在各个方向上是否一致。在上文的例子中,数值方向的更新量在两个方向上相互抵消,从而减缓了在竖直方向上的移动幅度。相比之下,所有梯度在水平方向上为正。因此,我们可以采用稍大的学习率,可以在解决梯度下降的问题的同时更快收敛。
AdaGrad 算法
在梯度下降中,目标函数自变量的每一个元素在相同时间步都使用同一个学习率来自我迭代。如果学习率过小,那么梯度较小的维度梯度更新太慢;如果学习率过大, 那么容易在梯度过大的维度上发散(震荡)。与动量法不同,AdaGrad 算法根据自变量在每个维度的梯度值的大小来调整各个维度上的学习率,从而避免统一的学习率难以适应所有维度的问题。
在每一时间步 $t$,引入变量 $\vec{s}_t$(初始化为 $\vec{0}$),
$$ \vec{s}_t \leftarrow \vec{s}_{t-1} + \vec{g}_{t} \odot \vec{g}_t, $$
并将待优化参数 $\vec{x}_t$ 中每个元素的学习率通过按元素运算重新调整一下:
$$ \vec{x}_t \leftarrow \vec{x}_{t-1} - \frac{\eta}{\sqrt{\vec{s}_t + \epsilon}} \odot \vec{g}_t, $$
其中 $\eta$ 是学习率,$\epsilon$ 是为了维持数值稳定性而添加的常数,如 $10^{-6}$。
观察上式可发现,如果目标函数有关自变量中某个元素的偏导数一直都较大,那么该元素的学习率将下降较快;反之,如果目标函数有关自变量中某个元素的偏导数一直都较小, 那么该元素的学习率将下降较慢。因此,对于图 3 所示的问题,AdaGrad 可以保证竖直方向的学习率较小,从而减缓竖直方向上的震荡现象。
然而,由于 $\vec{s}_t$ 一直在累加按元素平方的梯度,自变量中每个元素的学习率在迭代过程中一直在降低(或不变)。所以,
当学习率在迭代早期降得较快且当前解依然不佳时,AdaGrad 算法在迭代后期由于学习率过小,可能较难找到一个有用的解。这个问题的解决办法是:
增大学习率的初值。图 4 给出了图示。
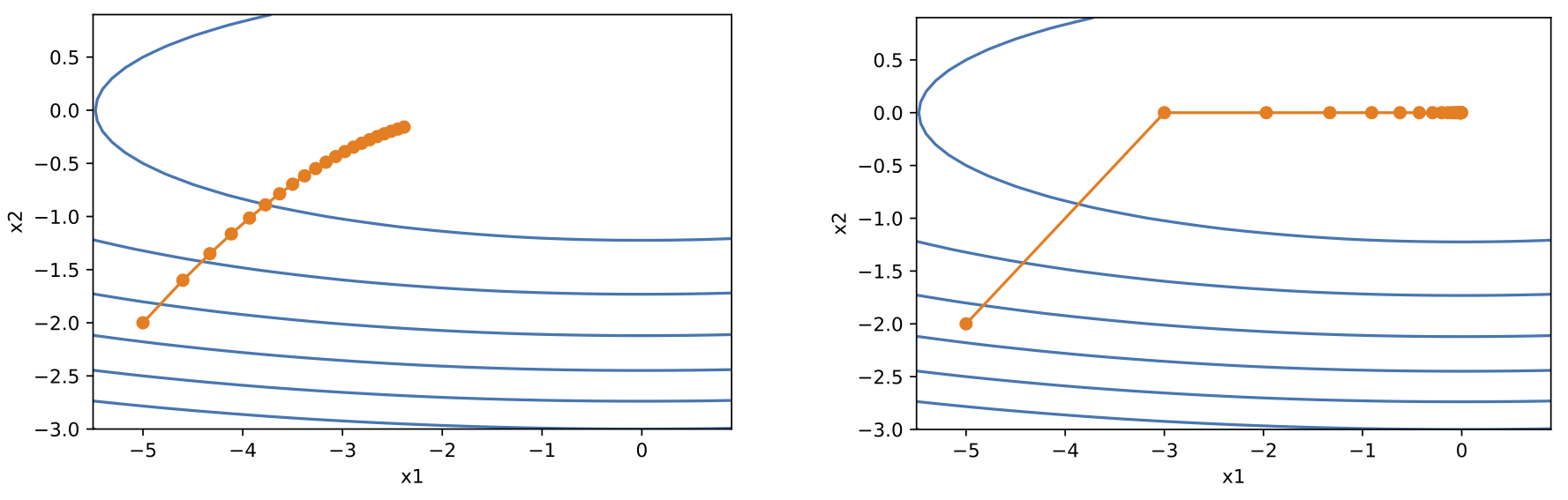
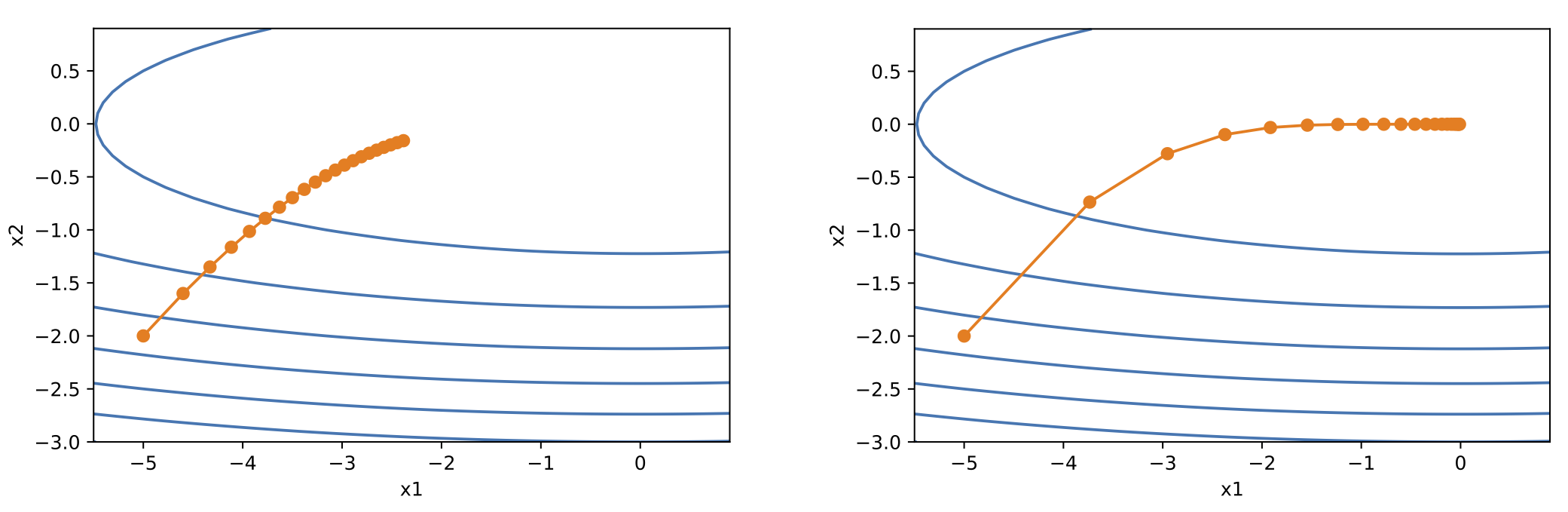
RMSProp 算法
AdaGrad 算法的问题是,当学习率在迭代早期降得较快且当前解依然不佳时,AdaGrad 算法在迭代后期由于学习率过小,可能较难找到一个有用的解。 虽然最简单的方式是增大学习率的初值,但是并未根除这个问题。造成这个问题的根本原因是学习率一直在减小。因此,可以对 AdaGrad 做一些调整,使得学习率不要一直降低。 这就是 RMSProp 的做法。
具体地,在每一时间步 $t$,变量 $\vec{s}_t$ 按如下方式更新:
$$ \vec{s}_t \leftarrow \gamma \vec{s}_{t-1} + (1 - \gamma) \vec{g}_{t} \odot \vec{g}_t, $$
其中 $\gamma \in [0,1)$。待优化参数 $\vec{x}_t$ 的更新方式保持不变:
$$ \vec{x}_t \leftarrow \vec{x}_{t-1} - \frac{\eta}{\sqrt{\vec{s}_t + \epsilon}} \odot \vec{g}_t, $$
其中 $\eta$ 是学习率,$\epsilon$ 是为了维持数值稳定性而添加的常数,如 $10^{-6}$。
此时 $\vec{s}_t$ 是对平方项 $\vec{g}_{t} \odot \vec{g}_t$ 的指数加权移动平均,因此 $\vec{s}_t$ 可能变大也可能变小,从而保证学习率不会一直减小。
AdaDelta 算法
对于 AdaGrad 算法的问题,与 RMSProp 不同,AdaDelta 算法是另一种改进方式。
具体地,在每一时间步 $t$,变量 $\vec{s}_t$ 按如下方式更新:
$$ \vec{s}_t \leftarrow \rho \vec{s}_{t-1} + (1 - \rho) \vec{g}_{t} \odot \vec{g}_t, $$
其中 $\rho \in [0,1)$。AdaDelta 额外维护了一个状态变量 $\Delta \vec{x}_t$(初始化为 $\vec{0}$),
用于代替 $\frac{\eta}{\sqrt{\vec{s}_t + \epsilon}} \odot \vec{g}_t$ 成为待学习参数 $\vec{x}_t$ 的变化量:
$$ \vec{g}'_t \leftarrow \sqrt{\frac{\Delta \vec{x}_{t-1} + \epsilon}{\vec{s}_t + \epsilon}} \odot \vec{g}_t, $$
其中 $\epsilon$ 是为了维持数值稳定性而添加的常数,如 $10^{-5}$。所以 $\vec{x}_t$ 的更新方式为:
$$ \vec{x}_t \leftarrow \vec{x}_{t-1} - \vec{g}'_t. $$
最后,更新状态变量 $\Delta \vec{x}_t$:
$$ \Delta \vec{x}_t \leftarrow \rho \Delta \vec{x}_{t-1} + (1 - \rho) \vec{g}'_t \odot \vec{g}'_t. $$
本质上,AdaDelta 是用 $\sqrt{\Delta \vec{x}_{t-1}}$ 代替学习率 $\eta$,相当于用过去的梯度的变化状态来学习一个较为合适的学习率。
Adam 算法
Adam 算法在 RMSProp 算法基础上对小批量随机梯度也做了指数加权移动平均,可以看做是 RMSProp 算法与动量法的结合。
给定超参数 $\beta_1 \in [0, 1)$(算法作者建议设为 0.9),时间步 $t$ 的动量变量 $\vec{v}_t$ 即小批量随机梯度 $\vec{g}_t$ 的指数加权移动平均:
$$ \vec{v}_t \leftarrow \beta_1 \vec{v}_{t-1} + (1 - \beta_1) \vec{g}_t. $$
再给定超参数 $\beta_2 \in [0, 1)$(算法作者建议设为 0.999), 对 $\vec{g}_t \odot \vec{g}_t$ 做指数加权移动平均:
$$ \vec{s}_t \leftarrow \beta_2 \vec{s}_{t-1} + (1 - \beta_2) \vec{g}_{t} \odot \vec{g}_t, $$
由于我们将 $\vec{v}_0$ 和 $\vec{s}_0$ 中的元素都初始化为 0, 在时间步 $t$ 我们得到
$$ \vec{v}_t = (1 - \beta_1) \sum_{i=1}^t \beta_1^{t-i} \vec{g}_i = (1 - \beta_1^t) \vec{g}_i. $$
显然,当 $t$ 较小时,过去各时间步小批量随机梯度权值之和会较小。为了消除这样的影响,通过除以 $(1 - \beta_1^t)$ 使各时间步小批量随机梯度权值之和为 1,这就是 “偏差修正”。对 $\vec{v}_t$ 和 $\vec{s}_t$ 做偏差修正:
$$ \begin{aligned} \hat{\vec{v}}_t &\leftarrow \frac{\vec{v}_t}{1 - \beta_1^t} \\ \hat{\vec{s}}_t &\leftarrow \frac{\vec{s}_t}{1 - \beta_2^t}. \end{aligned} $$
待学习参数 $\vec{x}_t$ 的变化量用修正后的变量计算:
$$ \vec{g}'_t \leftarrow \frac{\eta \hat{\vec{v}}_t}{\sqrt{\hat{\vec{s}}_t} + \epsilon}, $$
其中 $\eta$ 是学习率,$\epsilon$ 是为了维持数值稳定性而添加的常数,如 $10^{-8}$。
最后,更新待学习参数 $\vec{x}_t$:
$$ \vec{x}_t \leftarrow \vec{x}_{t-1} - \vec{g}'_t. $$
最后
本文提及的优化算法的 PyTorch 实现见本链接。
转载申请
本作品采用 知识共享署名 4.0 国际许可协议 进行许可,转载时请注明原文链接。您必须给出适当的署名,并标明是否对本文作了修改。