到目前为止,我们只定义了模型的正向传播(forward)的过程,梯度的反向传播则是 PyTorch 自动实现的。接下来将以带 $L_2$ 范数正则化项的、包含单个隐藏层的 MLP 解释反向传播的数学原理。
正向传播
不考虑偏置,设输入 $\vec{x} \in \mathbb{R}^d$,则得到中间变量 $\vec{z} = W^{(1)} \vec{x} \in \mathbb{R}^h$,
其中 $W^{(1)} \in \mathbb{R}^{h \times d}$ 为隐藏层的权重,其中 $h$ 是隐藏层神经元的个数;
$\vec{z}$ 作为输入传递给激活函数 $\phi$,得到 $\vec{h} = \phi(\vec{z}) \in \mathbb{R}^h$;
将 $\vec{h}$ 传递给输出层,得到 $\vec{o} = W^{(2)} \vec{h} \in \mathbb{R}^q$,其中 $W^{(2)} \in \mathbb{R}^{q \times h}$ 为输出层的权重,$q$ 为输出层神经元的个数(即 label 的个数)。
设损失函数为 $l$,且样本标签为 $y$,则单个样本的 loss 为 $L = l(\vec{o},y)$。考虑 $L_2$ 正则化项 $s = \frac{\lambda}{2} \left( \Vert W^{(1)} \Vert^2_F + \Vert W^{(2)} \Vert^2_F \right)$,则单个样本上的优化目标为
$$ J = L + s = l(\vec{o},y) + \frac{\lambda}{2} \left( \Vert W^{(1)} \Vert^2_F + \Vert W^{(2)} \Vert^2_F \right). $$
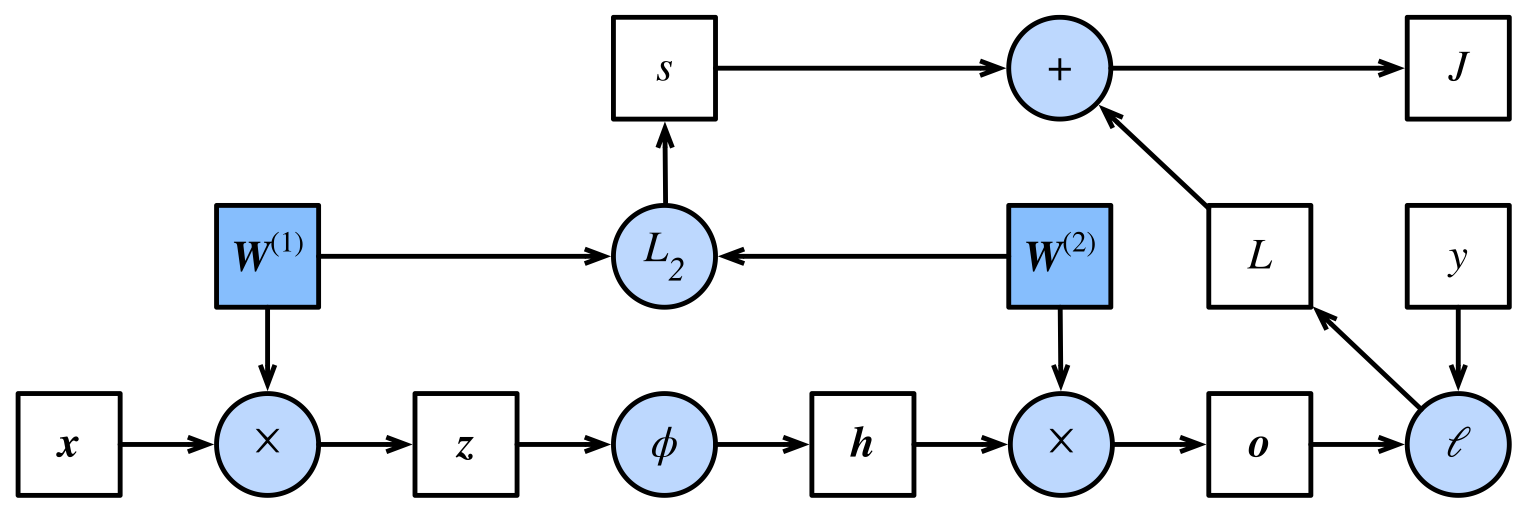
正向传播的计算图如下:
反向传播
反向传播依据微积分中的链式法则,沿着从输出层到输入层的顺序,依次计算并存储目标函数有关神经网络各层的中间变量以及参数的梯度。
第 $l$ 层的误差可由第 $l+1$ 层的误差得到,充分利用之前的计算结果。
张量求导的链式法则
对于任意形状的张量 $X,Y,Z$,若 $Y = f(X), Z = f(Y)$,则
$$
\frac{\partial Z}{\partial X} = \textrm{prod} \left(\frac{\partial Z}{\partial Y}, \frac{\partial Y}{\partial X} \right),
$$
其中 $\textrm{prod}(\cdot)$ 运算符将根据两个输入的形状,在必要的操作(如转置和互换输入位置)后对两个输入做乘法。
计算 $\frac{\partial J}{\partial W^{(2)}}$
将应用链式法则依次计算各中间变量和参数的梯度,其计算次序与前向传播中相应中间变量的计算次序恰恰相反。
首先 $J = L + s$(简单起见,仅考虑单个样本),所以 $ \frac{\partial J}{\partial L} = 1, \frac{\partial J}{\partial s} = 1$;
其次,由于 $L = l(\vec{o}, y)$,所以 $\frac{\partial J}{\partial \vec{o}} = \textrm{prod} \left( \frac{\partial J}{\partial L}, \frac{\partial L}{\partial \vec{o}} \right) = \frac{\partial L}{\partial \vec{o}}$;
因为 $s = \frac{\lambda}{2} \left( \Vert W^{(1)} \Vert^2_F + \Vert W^{(2)} \Vert^2_F \right)$,所以 $\frac{\partial s}{\partial W^{(1)}} = \lambda W^{(1)}$,$\frac{\partial s}{\partial W^{(2)}} = \lambda W^{(2)}$。因为 $\vec{o} = W^{(2)} \vec{h}$,所以 $\frac{\partial \vec{o}}{\partial (W^{(2)})^\textrm{T}} = \vec{h}$。
因此
$$ \frac{\partial J}{\partial W^{(2)}} = \textrm{prod} \left( \frac{\partial J}{\partial \vec{o}}, \frac{\partial \vec{o}}{\partial W^{(2)}} \right) + \textrm{prod} \left( \frac{\partial J}{\partial s}, \frac{\partial s}{\partial W^{(2)}} \right) = \textrm{prod} \left( \frac{\partial L}{\partial \vec{o}}, \vec{h} \right) + \lambda W^{(2)}. $$
计算 $\frac{\partial J}{\partial W^{(1)}}$
因为 $\frac{\partial \vec{o}}{\partial \vec{h}} = (W^{(2)})^\textrm{T}$,
所以 ${\frac{\partial J}{\partial \vec{h}}} = \textrm{prod} \left(\frac{\partial L}{\partial \vec{o}}, (W^{(2)})^\textrm{T} \right)$;
进一步地,$\frac{\partial J}{\partial \vec{z}} = \textrm{prod} \left( \frac{\partial J}{\partial h}, \frac{\partial h}{\partial z} \right) = \textrm{prod}\left(\frac{\partial L}{\partial \vec{o}}, (W^{(2)})^\textrm{T}\right) \odot \phi'(\vec{z})$;
最终,
$$ \begin{aligned} \frac{\partial J}{\partial W^{(1)}} &= \textrm{prod} \left(\frac{\partial J}{\partial \vec{z}}, \frac{\partial \vec{z}}{\partial W^{(1)}} \right) + \textrm{prod}\left(\frac{\partial J}{\partial s}, \frac{\partial s}{\partial W^{(1)}}\right) \\ &= \textrm{prod}\left(\textrm{prod}\left(\frac{\partial L}{\partial \vec{o}}, (W^{(2)})^\textrm{T}\right) \odot \phi' \left(\vec{z} \right), \vec{x}\right) + \lambda W^{(1)}. \end{aligned} $$
在模型参数初始化完成后,我们交替地进行正向传播和反向传播,并根据反向传播计算的梯度迭代模型参数。 我们在反向传播中使用了正向传播中计算得到的中间变量来避免重复计算,这导致正向传播结束后不能立即释放中间变量内存,因此训练要比预测占用更多的内存。 另外需要指出的是,这些中间变量的个数大体上与网络层数线性相关,每个变量的大小跟批量大小和输入个数也是线性相关的,它们是导致较深的神经网络使用较大批量训练时更容易超内存的主要原因。
最后
本文所使用的图片来自《动手学深度学习》(PyTorch 版)章节 3.14。
转载申请
本作品采用 知识共享署名 4.0 国际许可协议 进行许可,转载时请注明原文链接。您必须给出适当的署名,并标明是否对本文作了修改。