在讲解 MLP 时我们给出了如下图所示的带有隐藏层的神经网络:
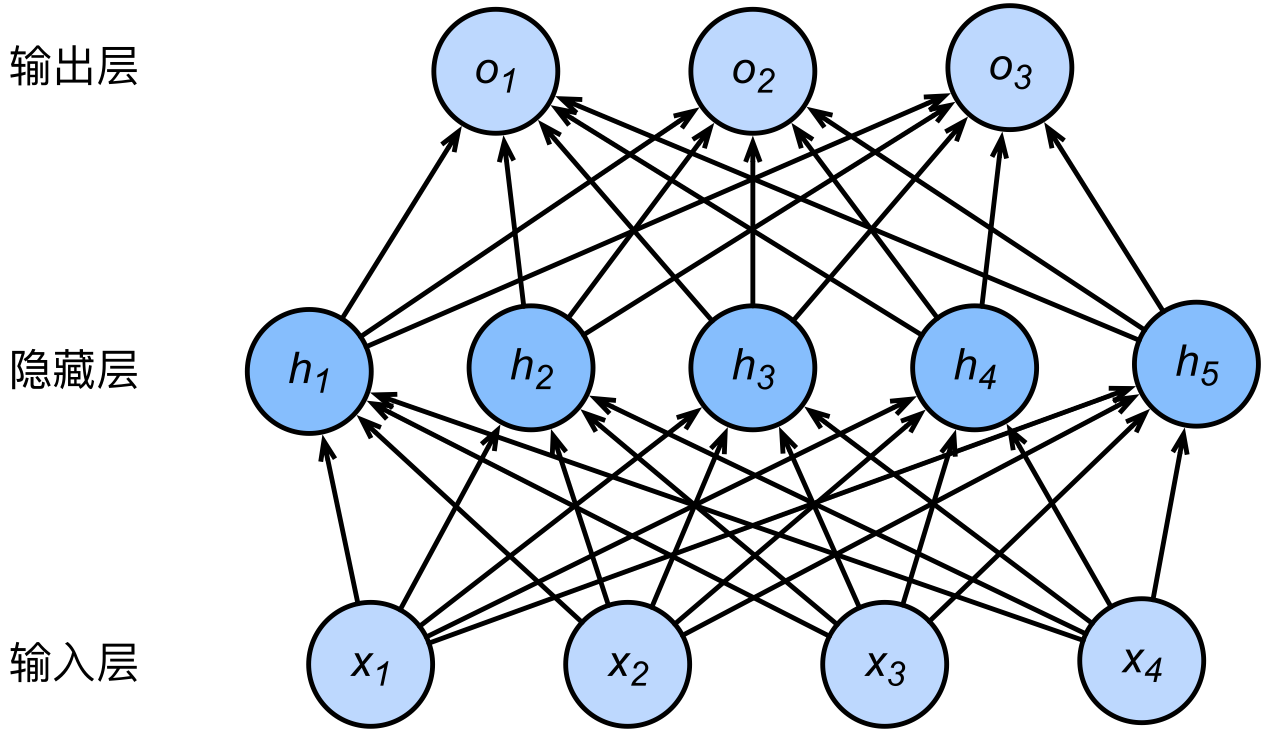
其中,对于单个样本 $\big([x_1, ..., x_4]^\top, y\big)$,隐藏单元 $h_i$ 的计算表达式为
$$ h_i = \phi \left(\vec{x}^\top W_h(:,i) + \vec{b_h}(i)\right). $$
若对该隐藏层使用 dropout,则该层的每个隐藏单元有一定概率会被丢弃掉。设丢弃概率(超参数)为 $p$,则 $\forall i, h_i$ 有 $p$ 的概率会被清零,有 $1-p$ 的概率会被做拉伸。用数学语言描述即
$$ h'_i = \frac{\xi_i}{1-p}h_i, $$
其中 $\xi_i$ 是一个随机变量,$p(\xi_i = 0) = p$,$p(\xi_i=1) = 1-p$。
则
$$ \mathbb{E} \left[ h'_i \right] = h_i. $$
这意味着 dropout 不改变输入的期望输出(这就是要除以 $1-p$ 的原因)。
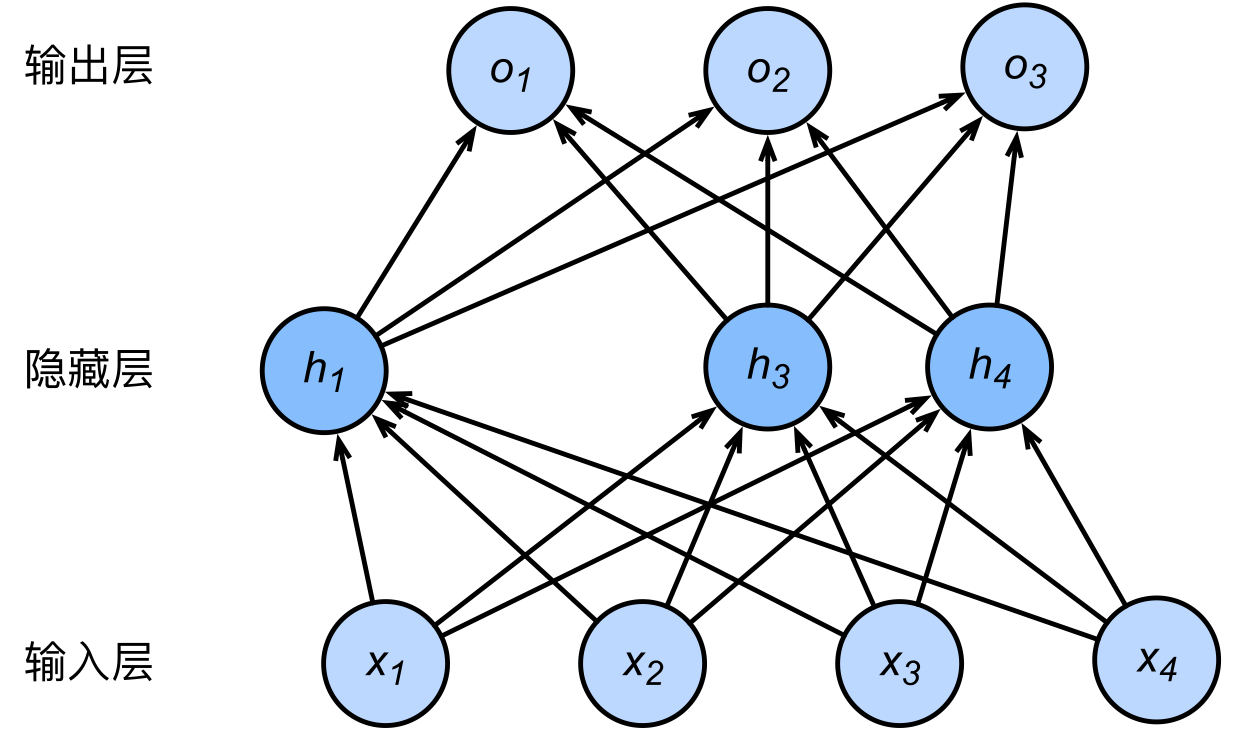
下图给出了 dropout 的一个示例。
此时 MLP 的输出不依赖 $h_2$ 和 $h_5$。由于在训练中隐藏层神经元的丢弃是随机的,即 $h_1, ..., h_5$ 都有可能被清零,输出层的计算无法过度依赖 $h_1, ..., h_5$ 中的任一个,
从而在训练模型时起到正则化的作用,并可以用来应对过拟合。
Dropout 是一种训练时应对过拟合的方法,并未改变网络的结构。当参数训练完毕并用于测试时,任何参数都不会被 dropout。
最后
本文所使用的图片分别来自《动手学深度学习》(PyTorch 版)章节 3.8 和章节 3.13。
Dropout 的 PyTorch 实现见 本链接 。
转载申请
本作品采用 知识共享署名 4.0 国际许可协议 进行许可,转载时请注明原文链接。您必须给出适当的署名,并标明是否对本文作了修改。