理解共轭梯度法（下）· 共轭梯度法

本文将重点介绍共轭梯度法（以下简称 CG）。关于梯度法的内容，请移步上篇理解共轭梯度法（上）· 梯度法及其分析。

3 共轭方向法

3.1 什么是共轭

观察理解共轭梯度法（上）· 梯度法及其分析图 7 中的 (b)，可发现在梯度法中，同一个迭代方向可能会反复出现。这意味着，对于重复出现的方向，对应的迭代 没有完全消除误差向量在这个方向上的分量。如果我们能找到 $n$ 个相互正交的搜索方向 $\vec{d}_{(0)},\vec{d}_{(1)}, \cdots, \vec{d}_{(n-1)}$ ，在每个方向上只移动一步即可完美消除误差向量在这个方向上的分量，那么只需要 $n$ 轮迭代即可收敛到全局最优，复杂度将会大大降低。

和梯度法一样，在共轭方向法中， $\vec{x}_{(i)}$ 将会按照如下的迭代式进行更新： $$ \begin{equation} \vec{x}_{(i+1)} \leftarrow \vec{x}_{(i)} + \alpha_{(i)} \vec{d}_{(i)}. \tag{e.q. 19} \end{equation} $$ 那么问题来了，如何按照上述思想求解出 $\alpha_{(i)}$ 和 $\vec{d}_{(i)}$ 呢？本质上，完全消除误差向量在各个搜索方向的分量，等价于 $$ \begin{equation} -\vec{e}_{(0)} = \vec{x}^\star - \vec{x}_{(0)} = \alpha_{(0)} \cdot \vec{d}_{(0)} + \cdots \alpha_{(n-1)} \cdot \vec{d}_{(n-1)}, \end{equation} $$ 即 “反向的初始误差向量 $-\vec{e}_{(0)}$ ” 可由各个搜索方向的线性组合表示，各搜索方向上的系数就是该方向上的搜索步长。由此可知第 $i+1$ 轮时的误差向量可表示为

$$ \begin{equation} \begin{split} \vec{e}_{(i+1)} &= \vec{e}_{(0)} + \sum_{k=0}^i \alpha_{(k)} \vec{d}_{(k)} \\ &= -\sum_{k=i+1}^{n-1} \alpha_{(k)} \vec{d}_{(k)}, \end{split} \tag{e.q. 20} \end{equation} $$

所以 $$ \begin{equation} \begin{split} \vec{d}_{(i)} \cdot \vec{e}_{(i+1)} &= -\sum_{k=i+1}^n \alpha_{(k)} \vec{d}_{(i)}^\mathrm{T} \vec{d}_{(k)} \\ &= 0. \qquad \vartriangleright \vec{d}_{(i)}^\mathrm{T} \vec{d}_{(j)} = 0 \textrm{ if } i \neq j \end{split} \tag{e.q. 21} \end{equation} $$ 这表明本轮的误差向量和上一轮的搜索方向必然正交。从而 $$ \begin{equation} \begin{split} \vec{d}_{(i)}^\mathrm{T} (\vec{e}_{(i)} + \alpha_{(i)} \vec{d}_{(i)}) &= 0 \quad \Longrightarrow \\ \alpha_{(i)} &= - \frac{\vec{d}_{(i)}^\mathrm{T} \vec{e}_{(i)}}{\vec{d}_{(i)}^\mathrm{T} \vec{d}_{(i)}}. \end{split} \tag{e.q. 22} \end{equation} $$ $(\textrm{e.q. 22})$ 给出了每一轮最优的迭代步长，这其实就是 “反向误差向量 $-\vec{e}_{(i)}$ ” 在第 $i$ 个搜索方向上投影的坐标值。但是， $\vec{e}_{(i)}$ 是未知的，即使给定了 $\vec{d}_{(i)}$ ，我们仍不知道 $\alpha_{(i)}$ 该如何计算。解决办法是把 “找到 $n$ 个相互正交的搜索方向 $\vec{d}_{(0)},\vec{d}_{(1)}, \cdots, \vec{d}_{(n-1)}$ ” 转变为 “找到 $n$ 个相互 $\mathbf{A}$ -正交的搜索方向 $\vec{d}_{(0)},\vec{d}_{(1)}, \cdots, \vec{d}_{(n-1)}$ ”。其中， $\mathbf{A}$ -正交（A-orthogonal）的定义为：若两个向量 $\vec{p}$ 和 $\vec{q}$ 满足 $$ \begin{equation} \vec{p}^\mathrm{T} \mathbf{A} \vec{q} = 0, \end{equation} $$ 则称 $\vec{p}$ 和 $\vec{q}$ 是 $\mathbf{A}$ -正交的。在这个新的思路下，我们可以真正地计算出 $\alpha_{(i)}$ 。不过，在此之前，我们先深入理解一下 $\mathbf{A}$ -正交这个概念。如图 9（图片的编号承接上篇）所示，(a) 是一般的 $\mathbf{A}$ -正交的向量对的样子，显然这些向量对并不正交。当 $\mathbf{A}$ 是对称阵且所有特征值都相同时，通过特征值分解可发现 $\vec{p}$ 和 $\vec{q}$ 正交，如 (b) 所示。从 (a) 到 (b) 可以理解为把能量范数小的特征向量拉伸到和能量范数大的特征向量一样长。

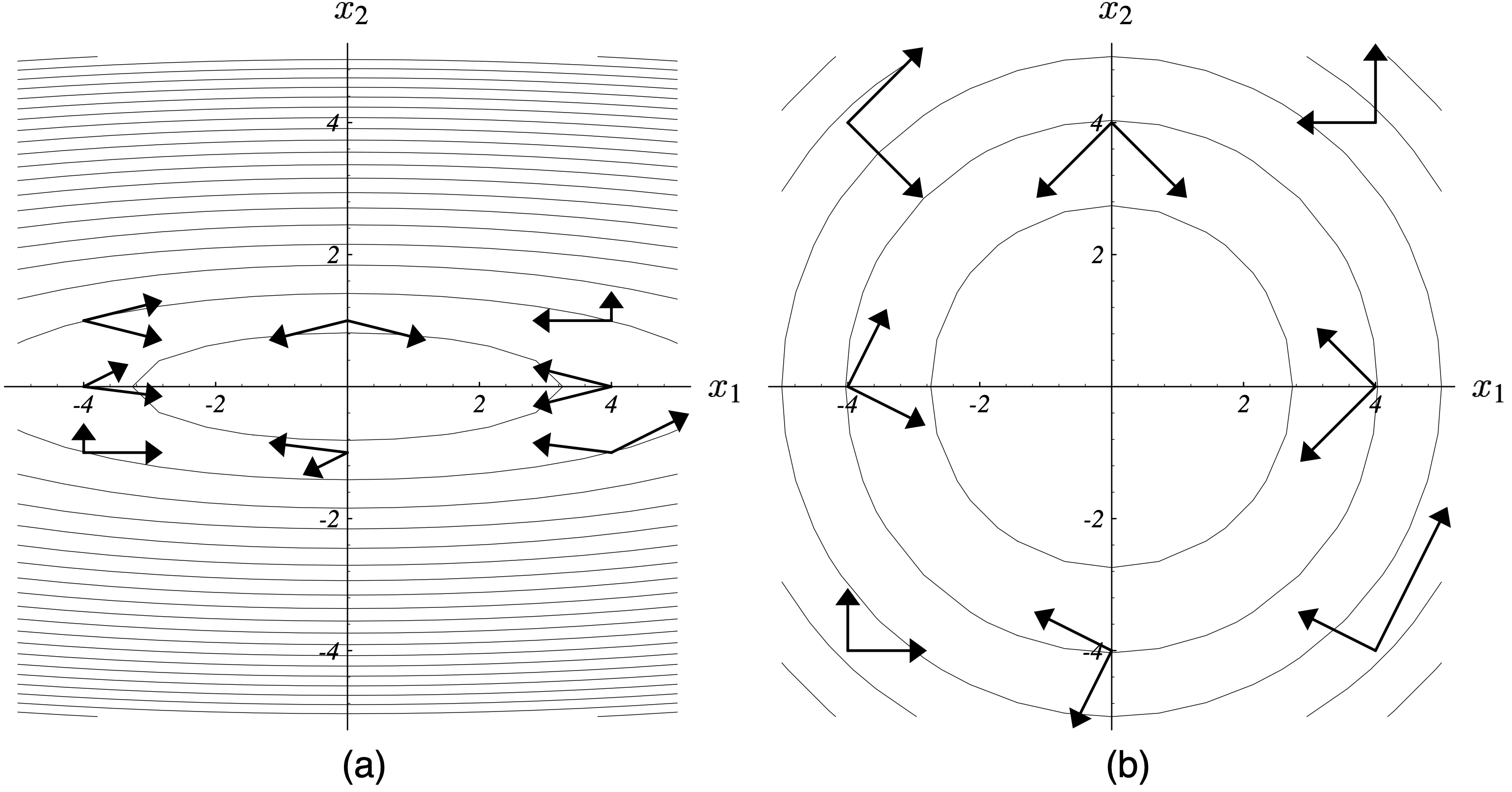
图 9 左图：$ \mathbf{A} $-正交的向量对；右图：变换过后的、$ \mathbf{A} $-正交的向量对。

这类 “通过相互 $\mathbf{A}$ -正交的搜索方向来找到最优解” 的方法就被统称为 共轭方向法（conjugate directions methods）。把上面的数学分析搬过来，可以得到和 $(\textrm{e.q. 21})$ 类似的结论：

$$ \begin{equation} \vec{d}_{(i)}^\mathrm{T} \mathbf{A} \vec{e}_{(i+1)} = 0. \tag{e.q. 23} \end{equation} $$

同样地，最优步长的结果也和 $(\textrm{e.q. 22})$ 类似：

$$ \begin{equation} \begin{split} \alpha_{(i)} &= - \frac{\vec{d}_{(i)}^\mathrm{T} \mathbf{A} \vec{e}_{(i)}}{\vec{d}_{(i)}^\mathrm{T} \mathbf{A} \vec{d}_{(i)}} \\ &= \frac{\vec{d}_{(i)}^\mathrm{T} \vec{r}_{(i)}}{\vec{d}_{(i)}^\mathrm{T} \mathbf{A} \vec{d}_{(i)}} \qquad \vartriangleright \vec{r}_{(i)} = - \mathbf{A} \vec{e}_{(i)} \end{split} \tag{e.q. 24} \end{equation} $$

和 $(\textrm{e.q. 22})$ 不一样的是，只要搜索方向 $\vec{d}_{(i)}$ 定了， $(\textrm{e.q. 24})$ 是可以直接计算的。在继续分析共轭方向法之前，我们先看看 $(\textrm{e.q. 23})$ 意味着什么。在梯度法中，最优步长的选取是根据理解共轭梯度法（上）· 梯度法及其分析 $(\textrm{e.q. 4})$ 来执行的。类似地，当我们采用 $(\textrm{e.q. 19})$ 来更新 $\vec{x}$ 的时候，就可以根据

$$ \begin{aligned} \nabla_{\alpha} f(\vec{x}_{(i+1)}) &= \big(\nabla_{\vec{x}_{(i+1)}} f(\vec{x}_{(i+1)})\big)^\mathrm{T} \nabla_{\alpha} \vec{x}_{(i+1)} \\ &= - \vec{r}_{(i+1)}^\mathrm{T} \vec{d}_{(i)} = - (\vec{d}_{(i)}^\mathrm{T} \vec{r}_{(i+1)})^\mathrm{T} = (\vec{d}_{(i)}^\mathrm{T} \mathbf{A} \vec{e}_{(i+1)})^\mathrm{T} = 0 \nonumber \end{aligned} $$

得到 $(\textrm{e.q. 23})$ ！这意味着梯度法中沿着搜索方向前进最优步长的过程就是对 $\mathbf{A}$ -正交性的运用。如果在每轮迭代中我们就将 $\vec{d}_{(i)}$ 设置为 $\vec{r}_{(i)}$ ，那么共轭方向法就退化成了梯度法。

和理解共轭梯度法（上）· 梯度法及其分析 $(\textrm{e.q. 11})$ 类似，我们采用搜索方向的线性组合来表示初始误差向量 $\vec{e}_{(0)}$ ：

$$ \begin{equation} \vec{e}_{(0)} = \sum_{i=0}^{n-1} \delta_i \vec{d}_{(i)}. \tag{e.q. 25} \end{equation} $$ 因为 $$ \begin{aligned} \vec{d}_{(j)}^\mathrm{T} \mathbf{A} \vec{e}_{(0)} &= \sum_{i=0}^{n-1} \delta_i \vec{d}_{(j)}^\mathrm{T} \mathbf{A} \vec{d}_{(i)} \\ &= \delta_j \vec{d}_{(j)}^\mathrm{T} \mathbf{A} \vec{d}_{(j)}, \qquad \vartriangleright \vec{d}_{(i)}^\mathrm{T} \mathbf{A} \vec{d}_{(j)} = 0 \textrm{ if } i \neq j \end{aligned} $$ 所以可得 $$ \begin{align} \delta_j &= \frac{\vec{d}_{(j)}^\mathrm{T} \mathbf{A} \vec{e}_{(0)}}{\vec{d}_{(j)}^\mathrm{T} \mathbf{A} \vec{d}_{(j)}} \\ &= \frac{\vec{d}_{(j)}^\mathrm{T} \mathbf{A} \vec{e}_{(0)} + \sum_{i=0}^{j-1} \alpha_{(i)} \vec{d}_{(j)}^\mathrm{T} \mathbf{A} \vec{d}_{(i)}}{\vec{d}_{(j)}^\mathrm{T} \mathbf{A} \vec{d}_{(j)}} \\ &= \frac{\vec{d}_{(j)}^\mathrm{T} \mathbf{A} \big( \vec{e}_{(0)} + \sum_{i=0}^{j-1} \alpha_{(i)} \vec{d}_{(i)} \big)}{\vec{d}_{(j)}^\mathrm{T} \mathbf{A} \vec{d}_{(j)}} && \vec{d}_{(i)}^\mathrm{T} \mathbf{A} \vec{d}_{(j)} = 0 \textrm{ if } i \neq j \\ &= \frac{\vec{d}_{(j)}^\mathrm{T} \mathbf{A} \vec{e}_{(j)}}{\vec{d}_{(j)}^\mathrm{T} \mathbf{A} \vec{d}_{(j)}} = - \frac{\vec{d}_{(j)}^\mathrm{T} \vec{r}_{(j)}}{\vec{d}_{(j)}^\mathrm{T} \mathbf{A} \vec{d}_{(j)}} && \vec{e}_{(j)} = \vec{e}_{(0)} + \sum_{i=0}^{j-1} \alpha_{(i)} \vec{d}_{(i)} \\ &= - \alpha_{(j)}. && \textrm{(e.q. 24)} \end{align} \tag{e.q. 26} $$

因此可以得到最优步长的等价计算公式： $\alpha_{(i)} = -\delta_{i}$ 。据此，我们可以对每一轮的误差向量 $\vec{e}_{(i)}$ 作如下等价变换：

$$ \begin{align} \vec{e}_{(i)} &= \vec{e}_{(0)} + \sum_{j=0}^{i-1} \alpha_{(j)} \vec{d}_{(j)} \\ &= \sum_{j=0}^{n-1} \delta_j \vec{d}_{(j)} - \sum_{j=0}^{i-1} \delta_{j} \vec{d}_{(j)} && \textrm{(e.q. 20)} \\ &= \sum_{j=i}^{n-1} \delta_j \vec{d}_{(j)}. && \textrm{(e.q. 25) & (e.q. 26)} \tag{e.q. 27} \end{align} $$ 这个公式表明共轭方向法的每轮迭代是在逐项消除误差向量的分量。这和本章节开头部分的分析完全一致。

3.2 共轭格莱姆 - 施密特过程

现在，只要每轮的迭代方向 $\vec{d}_{(i)}$ 确定，我们就能根据 $(\textrm{e.q. 19})$ 和 $(\textrm{e.q. 24})$ 来执行共轭方向法了。本章节将会采用 共轭格莱姆 - 施密特过程（conjugate Gram-Schmidt process）来确定这些相互 $\mathbf{A}$ -正交的迭代方向。

我们先来谈谈什么是 格莱姆 - 施密特过程（Gram-Schmidt process）。格莱姆 - 施密特过程是一个从任意一组线性无关的基 $\{\vec{u}_{(0)}, \cdots, \vec{u}_{(n-1)}\}$ 中构造出一组对应的（单位）正交基 $\{\vec{q}_{(0)}, \cdots, \vec{q}_{(n-1)}\}$ 的过程。具体地， $$ \begin{aligned} \vec{q}_{(0)} &= \vec{u}_{(0)}, \\ \vec{q}_{(1)} &= \vec{u}_{(1)} - \frac{\vec{u}_{(1)} \cdot \vec{q}_{(0)}}{\vec{q}_{(0)} \cdot \vec{q}_{(0)}} \vec{q}_{(0)}, \\ \qquad &\cdots \\ \vec{q}_{(n-1)} &= \vec{u}_{(n-1)} - \sum_{i=0}^{n-2} \left( \frac{\vec{u}_{(n-1)} \cdot \vec{q}_{(i)}}{\vec{q}_{(i)} \cdot \vec{q}_{(i)}} \vec{q}_{(i)} \right). \end{aligned} $$

以 $\vec{q}_{(1)}$ 的计算为例，以上过程就是将 $\vec{u}_{(1)}$ 进行正交分解，其中一个分量在 $\vec{q}_{(0)}$ 上，且系数为 $\frac{\vec{u}_{(1)} \cdot \vec{q}_{(0)}}{\vec{q}_{(0)} \cdot \vec{q}_{(0)}}$ （可通过 $\vec{u}_{(1)}$ 在 $\vec{q}_{(0)}$ 上的投影得到），另一个分量就是 $\vec{q}_{(1)}$ ，这样就能保证 $\vec{q}_{(1)}$ 和 $\vec{q}_{(0)}$ 是正交的。对于后续的 $\vec{u}_{(i)}$ 而言，在执行分解的时候，让 $i$ 个分量分别在 $\vec{q}_{(0)},\cdots,\vec{q}_{(i-1)}$ 上，最后剩下的就是 $\vec{q}_{(i)}$ 。如果要构造的是单位正交的一组基，那么 $\forall i, \vec{q}_{(i)}$ 按照如下方式计算：

$$ \begin{equation} \vec{q}_{(i)} = \vec{p}_{(i)} - \sum_{k=0}^{i-1} (\vec{p}_{(i)} \cdot \vec{q}_{(k)}) \vec{q}_{(k)}, \quad \vec{q}_{(i)} \leftarrow \frac{\vec{q}_{(i)}}{\Vert \vec{q}_{(i)} \Vert}. \end{equation} $$

把上述过程中的正交替换为 $\mathbf{A}$ -正交，即可得到共轭格莱姆 - 施密特过程。将 $\vec{q}_{(i)}$ 替换为 $\vec{d}_{(i)}$ ，即可得迭代方向的计算公式：

$$ \begin{equation} \forall i: \vec{d}_{(i)} = \vec{p}_{(i)} - \sum_{k=0}^{i-1} \bigg( \frac{\vec{p}_{(i)}^\mathrm{T} \mathbf{A} \vec{d}_{(k)}}{\vec{d}_{(k)}^\mathrm{T} \mathbf{A} \vec{d}_{(k)}} \vec{d}_{(k)} \bigg). \tag{e.q. 28} \end{equation} $$

我们将系数部分 $-\frac{\vec{p}_{(i)}^\mathrm{T} \mathbf{A} \vec{d}_{(k)}}{\vec{d}_{(k)}^\mathrm{T} \mathbf{A} \vec{d}_{(k)}}$ 定义为 $\beta_{ik}$ 。以上结论是直接套用格莱姆 - 施密特过程得到的，我们当然也可以手动推导出来这个结果。下面将给出推导过程。当 $i=0$ 时，直接取 $\vec{d}_{(i)} = \vec{p}_{(i)}$ 即可。对于之后的每一步（ $0 < i < n$ ），取

$$ \begin{equation} \vec{d}_{(i)} = \vec{p}_{(i)} + \sum_{k=0}^{i-1} \beta_{ik} \vec{d}_{(k)}, \tag{e.q. 29} \end{equation} $$

则

$$ \begin{equation} \begin{split} \vec{d}_{(i)}^\mathrm{T} \mathbf{A} \vec{d}_{(j)} &= \vec{p}_{(i)}^\mathrm{T} \mathbf{A} \vec{d}_{(j)} + \sum_{k=0}^{i-1} \Big( \beta_{ik} \vec{d}_{(k)}^\mathrm{T} \mathbf{A} \vec{d}_{(j)} \Big) \\ &= \vec{p}_{(i)}^\mathrm{T} \mathbf{A} \vec{d}_{(j)} + \beta_{ij} \vec{d}_{(j)}^\mathrm{T} \mathbf{A} \vec{d}_{(j)}, \end{split} \end{equation} $$

所以 $$ \begin{equation} \beta_{ij} = -\frac{\vec{p}_{(i)}^\mathrm{T} \mathbf{A} \vec{d}_{(j)}}{\vec{d}_{(j)}^\mathrm{T} \mathbf{A} \vec{d}_{(j)}}. \tag{e.q. 30} \end{equation} $$

结合 $(\textrm{e.q. 29})$ 和 $(\textrm{e.q. 30})$ 就得到了 $(\textrm{e.q. 28})$ 。

那么 $\vec{p}_{(i)}$ 如何设置呢？其实有很多选择。在 CG 中， $\vec{p}_{(i)} \leftarrow \vec{r}_{(i)}$ ，即迭代方向是由残差向量构造出来的！我在后面的章节会解释这样做的优越性。至此，共轭方向法所有理论细节已经准备完毕。不过，在给出算法描述之前，我们先来看看共轭方向法的最优性分析。

3.3 最优性分析

在允许的搜索范围内，每一轮迭代中，共轭方向法总可以让误差向量 $\vec{e}_{(i)}$ 的能量范数 $\Vert \vec{e}_{(i)} \Vert_{\mathbf{A}}$ 最小 [^1]。那么，什么是允许的搜索范围呢？不妨定义 $\mathcal{D}_i$ 为前 $i$ 个搜索方向所张成的空间，即 $\mathcal{D}_i \triangleq \textrm{span} \{ \vec{d}_{(0)}, \cdots, \vec{d}_{(i-1)} \}$ ，则根据 $(\textrm{e.q. 20})$ 有

$$ \begin{equation} \vec{e}_{(i)} = \vec{e}_{(0)} + \sum_{i=0}^{j-1} \alpha_{(i)} \vec{d}_{(i)} \in \vec{e}_{(0)} + \mathcal{D}_i. \end{equation} $$ 图 10 给了一个切实的案例来帮助理解 $\Vert \vec{e}_{(i)} \Vert_{\mathbf{A}}$ （ $i=2$ ）是如何被最小化的。

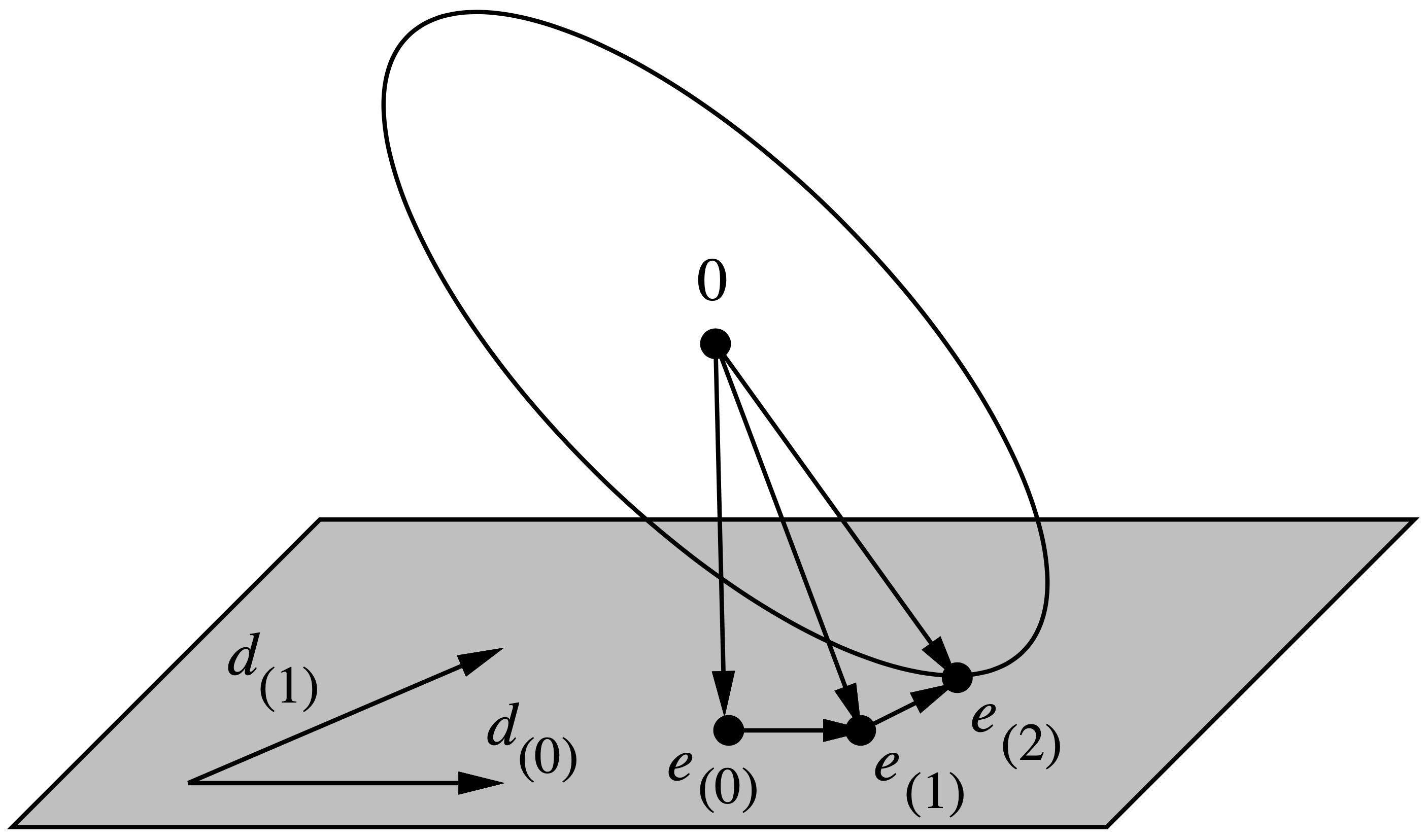
图 10 阴影区域为 $\vec{e}_{(0)} + \mathcal{D}_2$，椭圆是和该区域相切的 $\Vert \vec{e}_{(i)} \Vert_{\mathbf{A}} $ 的能量范数等高线。共轭方向法可以理解为 “通过在 $\vec{e}_{(0)} + \mathcal{D}_i$ 上找到合适的 $\vec{e}_{(i)}$ 来最小化当前解和最优解之间的差距”，即 $\vec{e}_{(i)} = \operatorname{argmin}_{\vec{e} \in \vec{e}_{(0)} + \mathcal{D}_i} \Vert \vec{e} \Vert_\mathbf{A}$。

接下来我们从理论上证明为什么在每一轮迭代中，共轭方向法都能做到最小化 $\Vert \vec{e}_{(i)} \Vert_{\mathbf{A}}$ 。我们将 $\Vert \vec{e}_{(i)} \Vert_{\mathbf{A}}^2$ 表示成累加的形式：

$$ \begin{align} \Vert \vec{e}_{(i)} \Vert^2_{\mathbf{A}} &= \vec{e}_{(i)}^\mathrm{T} \mathbf{A} \vec{e}_{(i)} \\ &= \Big(\sum_{j=i}^{n-1} \delta_j \vec{d}_{(j)} \Big)^\mathrm{T} \mathbf{A} \Big( \sum_{k=i}^{n-1} \delta_k \vec{d}_{(k)} \Big) && \textrm{(e.q. 27)} \\ &= \sum_{j=i}^{n-1} (\delta_j \vec{d}_{(j)})^\mathrm{T} \mathbf{A} (\delta_j \vec{d}_{(j)}). && \vec{d}_{(i)}^\mathrm{T} \mathbf{A} \vec{d}_{(j)} = 0 \textrm{ if } i \neq j \end{align} $$

仔细观察上式，可发现 $\Vert \vec{e}_{(i)} \Vert^2_{\mathbf{A}}$ 全部由尚未搜索过的方向的能量范数组成。这意味着 但凡是搜索过的方向，误差在该方向上的分量都已经被消除。因此这样得到的 $\Vert \vec{e}_{(i)} \Vert_{\mathbf{A}}$ 必然是最小的。至此，最优性已经分析完毕。在给出 CG 之前，我们还有三个推论需要说明。

将 $(\textrm{e.q. 27})$ 中的 $i$ 替换为 $j$ （取 $j > i$ ），并在其左右两端分别左乘 $-\vec{d}_{(i)}^\mathrm{T} \mathbf{A}$ 可得

$$ \begin{equation} \begin{split} \vec{d}_{(i)}^\mathrm{T} \vec{r}_{(j)} = -\vec{d}_{(i)}^\mathrm{T} \mathbf{A} \vec{e}_{(j)} &= -\vec{d}_{(i)}^\mathrm{T} \mathbf{A} \sum_{k=j}^{n-1} \delta_k \vec{d}_{(k)} \\ &= - \sum_{k=j}^{n-1} \delta_k \vec{d}_{(i)}^\mathrm{T} \mathbf{A} \vec{d}_{(k)} \\ &= 0. \qquad \vartriangleright \vec{d}_{(i)}\textrm{ and }\vec{d}_{(k)}\textrm{ }\mathbf{A}\textrm{-orthogonal} \end{split} \tag{e.q. 31} \end{equation} $$

这说明在共轭方向法中，当 $j \in \{i+1,\cdots,n-1\}$ 时，残差向量 $\vec{r}_{(j)}$ 与迭代方向 $\vec{d}_{(0)},\cdots,\vec{d}_{(i)}$ 都正交（推论 1）。这是因为每当我们沿着某个方向迈出一步之后，后续过程中就不再会往这个方向走了。因此误差向量与之前的所有搜索方向永远是 $\mathbf{A}$ -正交的。又因为 $\vec{r}_{(j)} = -\mathbf{A} \vec{e}_{(j)}$ ，故残差向量也必定与已经搜索过的方向正交。

另外，在 $(\textrm{e.q. 29})$ 左右两端点乘 $\vec{r}_{(j)}$ （取 $j > i$ ）可得 $$ \begin{equation} \begin{split} \vec{d}_{(i)}^\mathrm{T} \vec{r}_{(j)} &= \vec{p}_{(i)}^\mathrm{T} \vec{r}_{(j)} + \sum_{k=0}^{i-1} \beta_{ik} \vec{d}_{(k)}^\mathrm{T} \vec{r}_{(j)} \qquad \Longleftrightarrow \\ 0 &= \vec{p}_{(i)}^\mathrm{T} \vec{r}_{(j)}, \end{split} \tag{e.q. 32} \end{equation} $$ 即在共轭方向法中，当 $j \in \{i+1,\cdots,n-1\}$ 时，残差向量 $\vec{r}_{(j)}$ 与 $\vec{p}_{(0)},\cdots,\vec{p}_{(i)}$ 都正交（推论 2）。在 $(\textrm{e.q. 29})$ 左右两端点乘 $\vec{r}_{(j)}$ （取 $j = i$ ）可得 $$ \begin{equation} \vec{d}_{(i)}^\mathrm{T} \vec{r}_{(i)} = \vec{p}_{(i)}^\mathrm{T} \vec{r}_{(i)}. \tag{e.q. 33} \end{equation} $$ 这就是（推论 3）。

最后，有一个很重要的等价变换会在后文用到，这里先给出。在理解共轭梯度法（上）· 梯度法及其分析的 算法 2 中，我们通过理解共轭梯度法（上）· 梯度法及其分析 $(\textrm{e.q. 5})$ 来减少了一次矩阵 - 向量乘法运算。这个降低复杂度的操作在共轭方向法中依然适用。具体地，我们将 $(\textrm{e.q. 19})$ 按照如下方式变换： $$ \begin{equation} \begin{split} &\vec{x}_{(k)} = \vec{x}_{(k-1)} + \alpha_{(k-1)} \cdot \vec{d}_{(k-1)} \quad \Longleftrightarrow \\ - \mathbf{A} \vec{x}_{(k)} + \vec{b} &= - (\mathbf{A} \vec{x}_{(k-1)} - \vec{b}) - \alpha_{(k-1)} \mathbf{A} \vec{d}_{(k-1)} \quad \Longleftrightarrow \\ &\vec{r}_{(k)} = \vec{r}_{(k-1)} - \alpha_{(k-1)} \mathbf{A} \vec{d}_{(k-1)}. \end{split} \tag{e.q. 34} \end{equation} $$ 上式表明我们可以用 $\vec{r}_{(k-1)} - \alpha_{(k-1)} \mathbf{A} \vec{d}_{(k-1)}$ 代替 $\vec{b} - \mathbf{A} \vec{x}_{(k)}$ 来更新 $\vec{r}_{(k)}$ 。因为 $\mathbf{A} \vec{d}_{(k-1)}$ 是之前就已经计算过并保存下来的结果，所以直接复用就可以减少一次矩阵 - 向量乘法运算。当然，也会出现舍入误差，因此需要定期用 $\vec{b} - \mathbf{A} \vec{x}_{(k)}$ 来更新。

3.4 共轭梯度法

我们已经在前文说过，CG 中，搜索方向 $\vec{d}_{(0)}, \cdots, \vec{d}_{(n-1)}$ 是由残差向量 $\vec{r}_{(0)}, \cdots, \vec{r}_{(n-1)}$ 根据共轭格莱姆 - 施密特过程构造出来的。此时， $(\textrm{e.q. 32})$ 变成了 $$ \begin{equation} \forall i \neq j: \quad \vec{r}_{(i)}^\mathrm{T} \vec{r}_{(j)} = 0. \tag{e.q. 35} \end{equation} $$ 在此基础上，采用 $(\textrm{e.q. 24})$ 计算迭代步长并根据 $(\textrm{e.q. 19})$ 更新 $\vec{x}$ 即可。

现在，我来解释一下选择用残差向量来构造迭代方向的优势在哪里。回顾 $(\textrm{e.q. 29})$ ，仔细观察这个式子，它意味着构造 $\vec{d}_{(i)}$ 的时候需要用到前面所有的迭代方向 $\vec{d}_{(0)},\cdots,\vec{d}_{(i-1)}$ ，所以每一个迭代方向都需要被存储下来。当 $n$ 很大的时候，时间和空间的开销都很大。当 $\vec{p}_{(i)}$ 被设置为 $\vec{r}_{(i)}$ 的时候，奇迹发生了：首先 $$ \begin{aligned} &\vec{r}_{(i)}^\mathrm{T} \vec{r}_{(j+1)} = \vec{r}_{(i)}^\mathrm{T} \vec{r}_{(j)} - \alpha_{(j)} \vec{r}_{(i)}^\mathrm{T} \mathbf{A} \vec{d}_{(j)} \qquad \vartriangleright \textrm{(e.q. 34)} \\ &\alpha_{(j)} \vec{r}_{(i)}^\mathrm{T} \mathbf{A} \vec{d}_{(j)} = \vec{r}_{(i)}^\mathrm{T} \vec{r}_{(j)} - \vec{r}_{(i)}^\mathrm{T} \vec{r}_{(j+1)} \qquad \vartriangleright \textrm{(e.q. 35)} \\ \end{aligned} $$

$$ \begin{equation} \begin{split} \vec{r}_{(i)}^\mathrm{T} \mathbf{A} \vec{d}_{(j)} &= \left\{ \begin{array}{cl} \frac{1}{\alpha_{(i)}} \vec{r}_{(i)}^\mathrm{T} \vec{r}_{(i)}, & i=j \\ -\frac{1}{\alpha_{(i-1)}} \vec{r}_{(i)}^\mathrm{T} \vec{r}_{(i)}, & i=j+1 \\ 1. & \textrm{otherwise} \end{array} \right. \end{split} \tag{e.q. 36} \end{equation} $$

进而可得 $$ \begin{equation} \beta_{ij} = \left\{ \begin{array}{cl} \frac{1}{\alpha_{(i-1)}} \frac{\vec{r}_{(i)}^\mathrm{T} \vec{r}_{(i)}}{\vec{d}_{(i-1)}^\mathrm{T} \mathbf{A} \vec{d}_{(i-1)}}, & j = i-1 \\ 1. & j < i-1 \end{array} \right. \qquad \vartriangleright \textrm{e.q. 30} \tag{e.q. 37} \end{equation} $$

这意味着除了最近一次的迭代方向的常系数不为零，其他都是零！因此，我们不再需要存储之前的搜索方向了，这使得时空开销显著降低。这一优势让 CG 在每一轮迭代中的时间和空间复杂度均从 $O(n^2)$ 降低到了 $O(m)$ ，其中 $m$ 是 $\mathbf{A}$ 中非零元素的数量。

当 $j=i-1$ 时，将 $\alpha_{(i-1)}$ 的取值代入， $\beta_{ij}$ 还可以进一步化简：

$$ \begin{equation} \begin{split} \beta_{ij} &= \frac{\vec{d}_{(i-1)}^\mathrm{T} \mathbf{A} \vec{d}_{(i-1)}}{\vec{d}_{(i-1)}^\mathrm{T} \vec{r}_{(i-1)}} \cdot \frac{\vec{r}_{(i)}^\mathrm{T} \vec{r}_{(i)}}{\vec{d}_{(i-1)}^\mathrm{T} \mathbf{A} \vec{d}_{(i-1)}} \qquad \vartriangleright \textrm{(e.q. 24)} \\ &= \frac{\vec{r}_{(i)}^\mathrm{T} \vec{r}_{(i)}}{\vec{d}_{(i-1)}^\mathrm{T} \vec{r}_{(i-1)}} \qquad \vartriangleright \textrm{(e.q. 33) & } \vec{p}_{(i-1)} \leftarrow \vec{r}_{(i-1)} \\ &= \frac{\vec{r}_{(i)}^\mathrm{T} \vec{r}_{(i)}}{\vec{r}_{(i-1)}^\mathrm{T} \vec{r}_{(i-1)}} \end{split} \tag{e.q. 38} \end{equation} $$

为了方便描述，我们直接将 $\beta_{ij}$ （ $j=i-1$ ）改写为 $\beta_{(i-1)}$ ，则 $(\textrm{e.q. 29})$ 更新为

$$ \begin{equation} \vec{d}_{(i+1)} = \vec{r}_{(i+1)} + \beta_{(i)} \vec{d}_{(i)}. \tag{e.q. 39} \end{equation} $$ 结合以上分析，我们终于得到了 CG 的算法描述——算法 3。

算法 3 共轭梯度法

3.5 收敛性分析

虽然 CG 在理论上只需要 $n$ 轮迭代即可结束，但是收敛性分析依然是有意义的。一方面是因为我们偷懒用 $(\textrm{e.q. 34})$ 来代替矩阵 - 向量运算会导致舍入误差越来越大，从而导致残差向量越来越失准；另一方面是因为 “删除误差”（cancellation error）会导致搜索向量逐渐丧失 $\mathbf{A}$ -正交性。

3.5.1 选择最佳的多项式

因为（共轭）格莱姆 - 施密特变换是不改变基所张成的空间的，即 $$ \begin{equation} \textrm{span} \{\vec{r}_{(0)}, \cdots, \vec{r}_{(i)}\} = \textrm{span} \{\vec{d}_{(0)}, \cdots, \vec{d}_{(i)} \} = \mathcal{D}_{i+1}, \end{equation} $$ 所以显然有 $\vec{r}_{(i)} \in \mathcal{D}_{(i+1)}$ 。此外，仔细观察 $(\textrm{e.q. 34})$ 可知，第 $i+1$ 轮迭代后的残差向量 $\vec{r}_{(i+1)}$ 可以表示成上一轮迭代的残差向量 $\vec{r}_{(i)}$ 和 $\mathbf{A} \vec{d}_{(i)}$ 的线性组合。因此， $\vec{r}_{(i+1)}$ 所在的张成子空间等于 $\vec{r}_{(i)}$ 所张成的子空间和子空间 $\mathbf{A} \mathcal{D}_i$ 的并集，即 $$ \begin{equation} \mathcal{D}_{i+2} = \mathcal{D}_{i+1} \cup \mathbf{A} \mathcal{D}_{i+1}. \end{equation} $$ 利用递归性可得

$$ \begin{equation} \begin{split} \mathcal{D}_i &= \mathcal{D}_{i-1} \cup \mathbf{A} \mathcal{D}_{i-1} \\ &= \mathcal{D}_1 \cup \mathbf{A} \mathcal{D}_1 \cup \mathbf{A}^2 \mathcal{D}_1 \cup \cdots \cup \mathbf{A}^{i-1} \mathcal{D}_1 \\ &= \textrm{span} \{ \vec{d}_{(0)}, \mathbf{A} \vec{d}_{(0)}, \cdots, \mathbf{A}^{i-1} \vec{d}_{(0)} \} \\ &= \textrm{span} \{ \vec{r}_{(0)}, \mathbf{A} \vec{r}_{(0)}, \cdots, \mathbf{A}^{i-1} \vec{r}_{(0)} \} \quad \vartriangleright \vec{r}_{(i)} = -\mathbf{A} \vec{e}_{(i)} \\ &= \textrm{span} \{ \mathbf{A} \vec{e}_{(0)}, \mathbf{A}^2 \vec{e}_{(0)}, \cdots, \mathbf{A}^{i} \vec{e}_{(0)} \}. \end{split} \end{equation} $$ 上述子空间称为 Krylov 子空间，它是一个通过 “将一个矩阵反复左乘一个向量” 构建起来的子空间。对于这个空间，在第 $i$ 轮迭代中，误差项可以表示成如下形式（用上述张成子空间来描述）： $$ \begin{equation} \vec{e}_{(i)} = \Big( \mathbf{I} + \sum_{k=1}^i \psi_k \mathbf{A}^k \Big) \vec{e}_{(0)}, \tag{e.q. 40} \end{equation} $$ 其中 $\psi_k$ 是一个关于 $\alpha_{(k)}$ 和 $\beta_{(k)}$ 的函数。我们可以将圆括号内的表达式视为一个关于矩阵 $\mathbf{A}$ 的多项式 $P_i(\mathbf{A})$ ，其参数既可以是矩阵，也可以是标量。若参数是一个标量 $\lambda$ ，则 $P_i(\lambda) = 1 + \sum_{k=1}^i \psi_k \lambda^k$ （因此 $P_i(0) = 1$ ）。所以 $(\textrm{e.q. 40})$ 可以写作 $\vec{e}_{(i)} = P_i(\mathbf{A}) \vec{e}_{(0)}$ 。和分析梯度法时所采取的策略一样，令 $\vec{v}_1, \cdots, \vec{v}_n$ 是 $\mathbf{A}$ 的单位正交的特征向量， $\lambda_1, \cdots, \lambda_n$ 是对应的特征值，并将误差向量 $\vec{e}_{(0)}$ 用特征向量的线性组合表示： $\vec{e}_{(0)} = \sum_{i=1}^n \xi_i \vec{v}_i$ ，那么有 $$ \begin{equation} \begin{split} \vec{e}_{(i)} &= \sum_{j=1}^n \xi_j P_i(\lambda_j) \vec{v}_j \qquad \vartriangleright P_i(\mathbf{A}) \vec{v}_j = P_i(\lambda_j) \vec{v}_j \\ \mathbf{A} \vec{e}_{(i)} &= \sum_{j=1}^n \xi_j P_i(\lambda_j) \lambda_j \vec{v}_j \\ \Vert \vec{e}_{(i)} \Vert_\mathbf{A}^2 &= \sum_{j=1}^n \xi_j^2 \big( P_i(\lambda_j) \big)^2 \lambda_j, \qquad \vartriangleright \Vert \vec{v}_j \Vert = 1 \end{split} \tag{e.q. 41} \end{equation} $$ 且 $\Vert \vec{e}_{(0)} \Vert_\mathbf{A}^2 = \sum_{j=1}^n \xi_j^2 \lambda_j$ （因为 $P_0(\cdot) \equiv 1$ ）。我们在前文分析过，在每一轮迭代中，CG 都能做到最小化 $\Vert \vec{e}_{(i)} \Vert_{\mathbf{A}}$ 。对应到 $(\textrm{e.q. 41})$ ，即 CG 每轮迭代都能找到使得 $\Vert \vec{e}_{(i)} \Vert_{\mathbf{A}}$ 最小的多项式 $P_i$ ，其收敛性和最坏的特征向量的收敛性一致。因此， $$ \begin{aligned} \Vert \vec{e}_{(i)} \Vert_\mathbf{A}^2 &\leq \min_{P_i} \max_{\lambda} \big( P_i(\lambda) \big)^2 \sum_{j=1}^n \xi_j^2 \lambda_j \\ &= \min_{P_i} \max_{\lambda} \big( P_i(\lambda) \big)^2 \Vert \vec{e}_{(0)} \Vert_\mathbf{A}^2. \end{aligned} $$

同样地，我们还是拿 $n=2$ 的情况分析看看。对于理解共轭梯度法（上）· 梯度法及其分析图 4 中的例子， $\lambda_1 = 7,\lambda_2 = 2$ ，图 11 解释了 CG 是如何最小化 $\max_{\lambda} \big( P_i(\lambda) \big)^2$ 的。在图 11-(a) 中， $i=0$ ，尚未开始迭代，因此和 $\Vert \vec{e}_{(0)} \Vert_\mathbf{A}^2$ 的比值恒为 1；在图 11-(b) 中， $i=1$ ，在 $P_i(0) =1$ 的约束下，一阶多项式必然长成这个样子： $P_1(\lambda) = a^\star \lambda + 1$ ，其中 $a^\star$ 必然满足 $$ a^\star = \operatorname{argmin} _a \max \big\{ (2a+1)^2, (7a+1)^2 \big\}, $$ 求解上式可得 $a^\star = -2/9$ 。所以最优的一阶多项式为 $P_1(\lambda) = -2/9 \lambda + 1$ ，此时误差项的能量范数小于其初始值的 5/9；在图 11-(c) 中， $i=2$ ，我们完全有把握找到经过 $(0, 1), (2, 0), (7, 0)$ 三个点的二阶多项式，因而第二轮一结束误差项的能量范数就是 0 了，表明迭代结束，最优解已找到。

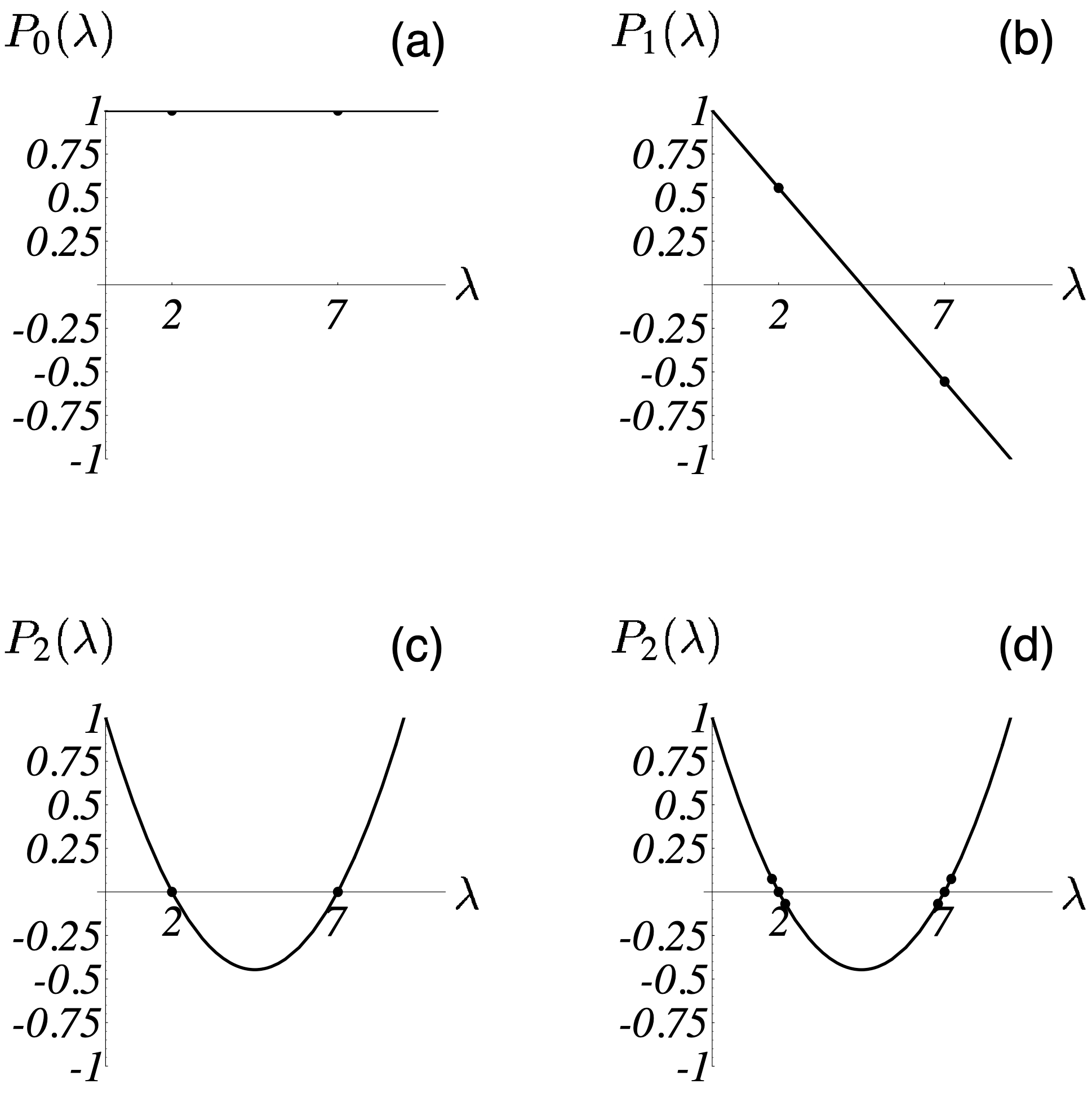
图 11 经过第 $i$ 轮之后，CG 的收敛情况取决于 “在 $P_i(0) =1$ 的约束下，$$ P_i $ 在各个特征值上距离 $ 0 $ 有多近”。

设想一下，若 $\lambda_1 = \lambda_2$ ，那么只需要一阶多项式即可拟合 $(0, 1), (\lambda_1, 0), (\lambda_2, 0)$ 三个点，这意味着一轮迭代就可以找到最优解了！这充分说明 CG 算法在特征值存在重复的情况下收敛是非常快的，重复的特征值越多，收敛速度越快。这一点和梯度法不谋而合。此外，如图 11-(d) 所示，当特征值不完全相同时，若这些特征值在 $\lambda_{min}$ 和 $\lambda_{max}$ 这两端分布较为集中，那么 CG 的收敛速度也不慢，因为此时也很容易找到一个多项式来拟合出一个不错的结果。

显然，特征值并不总是相同。因此，接下来我们将会分析最一般的情形，即特征值在 $[\lambda_{min}, \lambda_{max}]$ 之间均匀分布时，CG 的收敛速度如何。

3.5.2 切比雪夫多项式

我们首先引入一个著名的多项式，切比雪夫多项式（Chebyshev polynomials）。 $i$ 阶的切比雪夫多项式的表达式为 $$ \begin{equation} T_i (\omega) = \frac{1}{2} \Big( (\omega + \sqrt{\omega^2 -1})^i + (\omega - \sqrt{\omega^2 -1})^i \Big). \end{equation} $$

图 12 左图给出了切比雪夫不等式在不同的阶的情况下的图像。该多项式具有如下特性：

$\omega \in [-1, 1]$ 时， $｜T_i (\omega)｜ \leq 1$ ，其函数值在 - 1 到 1 之间反复震荡；
$\omega \notin [-1, 1]$ 时，其函数值尽其可能的迅速增长。

可以发现，当 $$ \begin{equation} P_i (\lambda) = \frac{T_i \Big( \frac{\lambda_{max} + \lambda_{min} - 2\lambda}{\lambda_{max} - \lambda_{min}}\Big)}{T_i \Big(\frac{\lambda_{max} + \lambda_{min}}{\lambda_{max} - \lambda_{min}}\Big)} \end{equation} $$ 时 [^2]，能够最小化 $\max_{\lambda} \big( P_i(\lambda) \big)^2$ 。图 12 右图给出了 $\lambda_{min}=2,\lambda_{max}=7$ 时上述多项式的图像。和图 11-(c) 相比，虽然两轮迭代后还不能收敛，但是已经是一个不错的结果：误差项的能量范式将不大于其初始值的 0.183 倍。

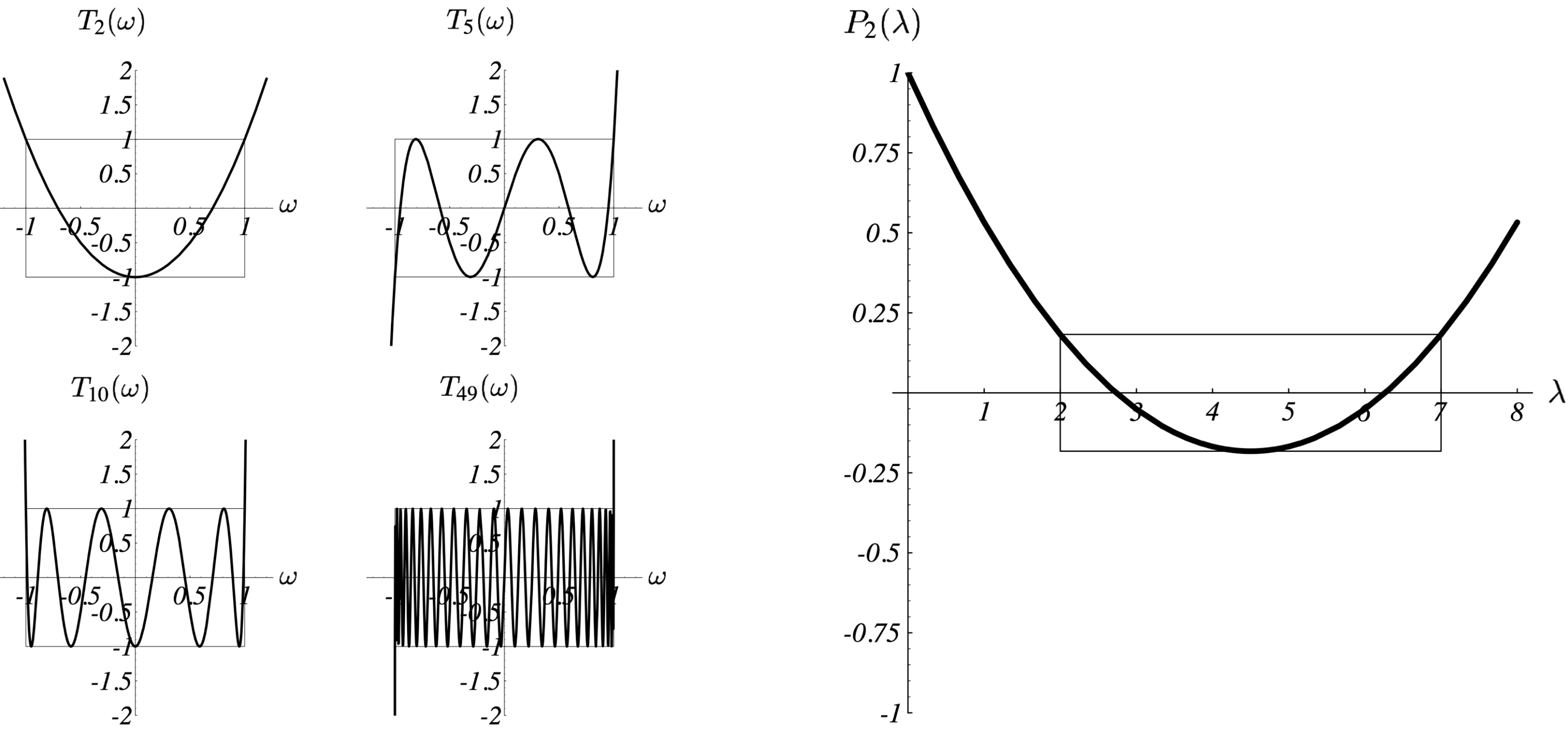
图 12 左图：切比雪夫不等式在不同的阶的情况下的图像；右图：一般情况下最小化能量范式二阶多项式示意图。

根据切比雪夫多项式的特性可知 $T_i(\frac{\lambda_{max} + \lambda_{min} - 2\lambda}{\lambda_{max} - \lambda_{min}}) \leq 1$ ，所以 $$ \begin{equation} \begin{split} \Vert \vec{e}_{(i)} \Vert_\mathbf{A} &\leq \frac{T_i \Big( \frac{\lambda_{max} + \lambda_{min} - 2\lambda}{\lambda_{max} - \lambda_{min}}\Big)}{T_i \Big(\frac{\lambda_{max} + \lambda_{min}}{\lambda_{max} - \lambda_{min}}\Big)} \Vert \vec{e}_{(0)} \Vert_\mathbf{A} \\ &\leq T_i \bigg(\frac{\lambda_{max} + \lambda_{min}}{\lambda_{max} - \lambda_{min}}\bigg)^{-1} \Vert \vec{e}_{(0)} \Vert_\mathbf{A} \\ &= 2 \bigg(\Big(\frac{\sqrt{\kappa}+1}{\sqrt{\kappa}-1}\Big)^i + \Big(\frac{\sqrt{\kappa}-1}{\sqrt{\kappa}+1}\Big)^i \bigg)^{-1} \Vert \vec{e}_{(0)} \Vert_\mathbf{A}. \end{split} \tag{e.q. 42} \end{equation} $$

随着 $i$ 的增加， $\Big(\frac{\sqrt{\kappa}+1}{\sqrt{\kappa}-1}\Big)^{-i}$ 会逐渐收敛到 0，因此更多的时候我们用下面的弱不等式来表述 CG 的收敛速度： $$ \begin{equation} \begin{split} \Vert \vec{e}_{(i)} \Vert_\mathbf{A} \leq 2 \Big(\frac{\sqrt{\kappa}-1}{\sqrt{\kappa}+1}\Big)^i \Vert \vec{e}_{(0)} \Vert_\mathbf{A}. \end{split} \tag{e.q. 43} \end{equation} $$ 我们可以对比一下 $(\textrm{e.q. 42})$ 和理解共轭梯度法（上）· 梯度法及其分析 $(\textrm{e.q. 18})$ ，可发现 $i=1$ 时二者相同。这是显然的，因为 CG 的第一步和梯度法一样。 $i>1$ 时，对比理解共轭梯度法（上）· 梯度法及其分析图 8 可发现 CG 通常要比梯度法快。图 13 给出了 CG 算法（每轮迭代）收敛性关于条件数 $\kappa$ 的函数图像，图上略掉了系数 2。实际应用中，由于较好的特征值分布或者比较理想的起始点的存在，CG 算法通常收敛的比 $(\textrm{e.q. 43})$ 所描述的还要快。

图 13 CG 算法（每轮迭代）收敛性关于条件数 $\kappa$ 的函数图像。

3.6 复杂度分析

上一章节分析了 CG 的收敛性，其收敛速度和 “特征值的取值是否相同” 以及 “条件数的大小” 有关。本章节将分析 CG 的复杂度。

就计算复杂度而言，不论是 CG 还是梯度法，其迭代过程中最耗时的操作都是矩阵 - 向量乘积。一般而言，矩阵 - 向量乘积需要 $O(m)$ 次操作，其中 $m$ 为矩阵非零元的个数。显然，矩阵越稀疏，这一操作的算力需求就越小。复杂度可以根据收敛速度得到。对于梯度法，假设我们希望执行足够多的迭代次数来把误差的能量范式减少到其初始值的 $\epsilon$ 倍，即 $\Vert \vec{e}_{(i)} \Vert = \epsilon \Vert \vec{e}_{(0)} \Vert$ ，则根据理解共轭梯度法（上）· 梯度法及其分析 $(\textrm{e.q. 18})$ 可算出梯度法实现这个边界条件的最大迭代次数需求为

$$ \begin{equation} i \leq \bigg \lceil \frac{1}{2} \kappa \ln \Big(\frac{1}{\epsilon}\Big) \bigg \rceil. \end{equation} $$

类似地，根据 $(\textrm{e.q. 43})$ 可算出 CG 实现这个边界条件的最大迭代次数需求为 $$ \begin{equation} i \leq \bigg \lceil \frac{1}{2} \sqrt{\kappa} \ln \Big(\frac{2}{\epsilon}\Big) \bigg \rceil. \end{equation} $$

因此，

时间复杂度：梯度法为 $O(m \kappa)$ ，CG 为 $O(m \sqrt{\kappa})$ ；
空间复杂度，二者均为 $O(m)$ 。

二阶椭圆边值问题在 $d$ 维域上的有限差分和有限元逼近通常有： $\kappa \in O(n^{2/d})$ 。所以在二维问题上，梯度法的时间复杂度为 $O(n^2)$ ，CG 则为 $O(n^{3/2})$ ；在三维问题上，梯度法的时间复杂度为 $O(n^{5/3})$ ，CG 则为 $O(n^{4/3})$ 。

4 共轭梯度法的实现

本章节将谈一谈在实现 CG 时应当注意的一些细节问题，包括起始点和算法停止迭代的条件应如何选取、需要怎样的预处理等。

4.1 起点与终点

起始点 $\vec{x}_{(0)}$ 的选取对 CG 的影响其实并不大，一般取 $\vec{x}_{(0)} = \vec{0}$ 即可。对于给定的二次型 $f(\vec{x})$ 且 $\mathbf{A}$ 为对称正定阵时，任意初始点最终都必将收敛。但是对于非凸优化问题，因为存在多个局部极小值点，初始点的选取将极大影响最终结果。

观察 $(\textrm{e.q. 38})$ 和 算法 3 的 Step 14 可知，当残差向量为零的时候， $\beta_{ij}$ 的计算必然发生除零错误。因此算法需要在残差向量等于 $\vec{0}$ 之前停止迭代。但是，由于舍入误差的存在，可能会得到一个假的零残差。因此绝大多数时候，更稳妥的做法是当残差向量（的范数）小于某个给定阈值的时候就停下来。算法 3 的 Step 4 正是这样做的。

4.2 预处理

观察图 13 以及 $(\textrm{e.q. 43})$ ，可发现随着条件数 $\kappa$ 的增加，CG 收敛速度越来越慢。因此，如果可以降低给定矩阵的条件数，就可以让 CG 更快地收敛。设 $\mathbf{M}$ 是一个对称正定且方便求逆的矩阵，则求解 $\mathbf{A} \vec{x} = \vec{b}$ 等价于求解 $$ \begin{equation} \mathbf{M}^{-1} \mathbf{A} \vec{x} = \mathbf{M}^{-1} \vec{b}, \end{equation} $$ 若 $\kappa(\mathbf{M}^{-1} \mathbf{A}) \ll \kappa(\mathbf{A})$ （ $\mathbf{M}^{-1} \mathbf{A}$ 的特征值分布比 $\mathbf{A}$ 更集中）且 $\mathbf{M}^{-1} \mathbf{A}$ 对称正定，则用 CG 求解上式比直接求解 $\mathbf{A} \vec{x} = \vec{b}$ 更快。这就是 “预处理” 的思路， $\mathbf{M}$ 被称为 预处理器。但是，现实是残酷的，即使 $\mathbf{M}$ 和 $\mathbf{A}$ 都对称正定也无法保证 $\mathbf{M}^{-1} \mathbf{A}$ 对称正定。

实际上可以绕过这个问题。对于任意对称正定矩阵 $\mathbf{M}$ ，必然存在矩阵 $\mathbf{E}$ 满足 $\mathbf{E} \mathbf{E}^\mathrm{T} = \mathbf{M}$ （可通过 Cholesky 分解获得）。设 $\lambda$ 是 $\mathbf{M}^{-1} \mathbf{A}$ 的特征向量， $\vec{v}$ 是对应的特征向量，则 $$ \begin{align} (\mathbf{E}^{-1} \mathbf{A} \mathbf{E}^{-\mathrm{T}})(\mathbf{E}^{\mathrm{T}} \vec{v}) &= \mathbf{E}^{-1} \mathbf{A} (\mathbf{E}^{-\mathrm{T}} \mathbf{E}^{\mathrm{T}}) \vec{v} \\ &= (\mathbf{E}^{\mathrm{T}} \mathbf{E}^{-\mathrm{T}}) \mathbf{E}^{-1} \mathbf{A} \vec{v} = \mathbf{E}^{\mathrm{T}} (\mathbf{E}^{-\mathrm{T}} \mathbf{E}^{-1}) \mathbf{A} \vec{v} && \mathbf{E}^{-\mathrm{T}} \mathbf{E}^{\mathrm{T}} = \mathbf{E}^{\mathrm{T}} \mathbf{E}^{-\mathrm{T}} = \mathbf{I} \\ &= \mathbf{E}^{\mathrm{T}} \mathbf{M}^{-1} \mathbf{A} \vec{v} && \mathbf{E}^{-\mathrm{T}} \mathbf{E}^{-1} = \mathbf{M}^{-1} \\ &= \lambda (\mathbf{E}^{\mathrm{T}} \vec{v}), && \mathbf{M}^{-1} \mathbf{A} \vec{v} = \lambda \vec{v} \end{align} $$ 即 $\lambda$ 也是 $\mathbf{E}^{-1} \mathbf{A} \mathbf{E}^{-\mathrm{T}}$ 特征值，且相应的特征向量为 $\mathbf{E}^\mathrm{T} \vec{v}$ ！因此，求解 $\mathbf{A} \vec{x} = \vec{b}$ 等价于求解 $$ \begin{equation} \left\{ \begin{array}{l} \mathbf{E}^{-1} \mathbf{A} \mathbf{E}^{-\mathrm{T}} \hat{\vec{x}} = \mathbf{M}^{-1} \vec{b}, \\ \hat{\vec{x}} = \mathbf{E}^\mathrm{T} \vec{x}. \end{array} \right. \end{equation} $$ 我们可以先求解 $\hat{\vec{x}}$ ，再求解 $\vec{x}$ 。当 $\mathbf{A}$ 为对称正定阵时 $\mathbf{E}^{-1} \mathbf{A} \mathbf{E}^{-\mathrm{T}}$ 也是对称正定阵，因此可通过 CG 求解 $\hat{\vec{x}}$ 。这就是 “变换预处理共轭梯度法”（Transformed Preconditioned Conjugate Gradient Method，TPCG），在框架上和 CG 一致。 $(\textrm{e.q. 44})$ 总结了相关的要点。

$$ \begin{equation} \left\{ \begin{array}{l} \hat{\vec{d}}_{(0)} = \hat{\vec{r}}_{(0)} = \mathbf{E}^{-1} \vec{b} - \mathbf{E}^{-1} \mathbf{A} \mathbf{E}^{-\mathrm{T}} \hat{\vec{x}}_{(0)} \\ \alpha_{(i)} = \frac{\hat{\vec{r}}_{(i)}^\mathrm{T} \hat{\vec{r}}_{(i)}}{\hat{\vec{d}}_{(i)}^\mathrm{T} \mathbf{E}^{-1} \mathbf{A} \mathbf{E}^{-\mathrm{T}} \hat{\vec{d}}_{(i)}} \\ \hat{\vec{x}}_{(i+1)} = \hat{\vec{x}}_{(i)} + \alpha_{(i)} \hat{\vec{d}}_{(i)} \\ \hat{\vec{r}}_{(i+1)} = \hat{\vec{r}}_{(i)} - \alpha_{(i)} \mathbf{E}^{-1} \mathbf{A} \mathbf{E}^{-\mathrm{T}} \hat{\vec{d}}_{(i)} \\ \beta_{(i+1)} = \frac{\hat{\vec{r}}_{(i+1)}^\mathrm{T} \hat{\vec{r}}_{(i+1)}}{\hat{\vec{r}}_{(i)}^\mathrm{T} \hat{\vec{r}}_{(i)}} \\ \hat{\vec{d}}_{(i+1)} = \hat{\vec{r}}_{(i+1)} + \beta_{(i+1)} \hat{\vec{d}}_{(i)}. \end{array} \right. \tag{e.q. 44} \end{equation} $$

然而，TPCG 需要我们通过矩阵分解的方法计算出 $\mathbf{E}$ 。有没有什么办法可以避免 $\mathbf{E}$ 的计算并且直接计算 $\vec{x}$ 而非 $\hat{\vec{x}}$ 呢？有！令 $\hat{\vec{r}}_{(i)} = \mathbf{E}^{-1} \vec{r}_{(i)}$ 且 $\hat{\vec{d}}_{(i)} = \mathbf{E}^\mathrm{T} \vec{d}_{(i)}$ ，再利用等价变换 $\hat{\vec{x}} = \mathbf{E}^\mathrm{T} \vec{x}$ 和 $\mathbf{E}^{-\mathrm{T}} \mathbf{E}^{-1} = \mathbf{M}^{-1}$ 即可从 $(\textrm{e.q. 44})$ 得到

$$ \begin{equation} \left\{ \begin{array}{l} \vec{r}_{(0)} = \vec{b} - \mathbf{A} \vec{x}_{(0)}, \vec{d}_{(0)} = \mathbf{M}^{-1} \vec{r}_{(0)} \\ \alpha_{(i)} = \frac{\vec{r}_{(i)}^\mathrm{T} \mathbf{M}^{-\mathrm{T}} \vec{r}_{(i)}}{\vec{d}_{(i)}^\mathrm{T} \mathbf{A} \vec{d}_{(i)}} \\ \vec{x}_{(i+1)} = \vec{x}_{(i)} + \alpha_{(i)} \vec{d}_{(i)} \\ \vec{r}_{(i+1)} = \vec{r}_{(i)} - \alpha_{(i)} \mathbf{A} \vec{d}_{(i)} \\ \beta_{(i+1)} = \frac{\vec{r}_{(i+1)}^\mathrm{T} \mathbf{M}^{-1} \vec{r}_{(i+1)}}{\vec{r}_{(i)}^\mathrm{T} \mathbf{M}^{-1} \vec{r}_{(i)}} \\ \vec{d}_{(i+1)} = \mathbf{M}^{-1} \vec{r}_{(i+1)} + \beta_{(i+1)} \vec{d}_{(i)}. \end{array} \right. \tag{e.q. 45} \end{equation} $$

这就是 未变换预处理共轭梯度法（Untransformed Preconditioned CG Method，UPCG）。之所以叫做 “未变换的” 是因为和 TPCG 相比， UPCG 不需要变换为 $\hat{\vec{x}}$ 来求解。此外，UPCG 也不再需要计算 $\mathbf{E}$ 了，因为根本没用到这个变量。

本质上，预处理是尝试对二次型 $f(\vec{x})$ 的图形进行拉伸，使其更接近于球形，以便它的特征值彼此之间更加靠近。最完美的预处理器当然是 $\mathbf{M} = \mathbf{A}$ ，因为此时 $\kappa(\mathbf{M}^{-1} \mathbf{A}) = 1$ ，相当于把 $f(\vec{x})$ 沿着特征向量进行伸缩， $f(\vec{x})$ 被拉伸为一个完美的球形。但是，这样做毫无意义，因为经过预处理之后，我们还是要求解 $\mathbf{M} \vec{x} = \vec{b}$ （与原始问题等价）。一种常用的预处理器 $\mathbf{M}$ 是 $\mathbf{A}$ 对角元素组成的对角阵。这相当于把 $f(\vec{x})$ 沿着坐标轴进行伸缩。此外，之所以这样选择的另一个重要原因是它的逆很好求解。人们其实发明了很多预处理器，一种更为精细复杂的预处理器是 不完备 Cholesky 预处理（incomplete Cholesky preconditioning），本文不再详细介绍。

本章节所有的分析虽然是针对 CG 的，但是同样适用于梯度法。对应地，有 变换 / 未变换预处理最速下降法（Transformed/Untransformed Preconditioned Steepest Descent Method）。

4.3 扩展到一般场景

到目前为止，我们只讨论当 $\mathbf{A}$ 为对称正定阵的情形。对于一般的矩阵，可否将梯度法和 CG 用上呢？以最小二乘问题为例： $$ \begin{equation} \min_{\vec{x}} \Vert \mathbf{A} \vec{x} - \vec{b} \Vert^2, \tag{e.q. 46} \end{equation} $$ 其解可通过 $\nabla_{\vec{x}} \Vert \mathbf{A} \vec{x} - \vec{b} \Vert^2 = 0$ 得到，即 $$ \begin{equation} \mathbf{A}^\mathrm{T} \mathbf{A} \vec{x} = \mathbf{A}^\mathrm{T} \vec{b}. \tag{e.q. 47} \end{equation} $$ 若 $\mathbf{A}$ 为非奇异的方阵，则上式等价于 $\mathbf{A} \vec{x} = \vec{b}$ 。若 $\mathbf{A} \in \mathbb{R}^{m \times n}$ 且 $m > n$ （overconstrained），那么 $(\textrm{e.q. 47})$ 可能无解。但不论如何， $(\textrm{e.q. 46})$ 总是有解的。怎么求呢？我们知道 $\mathbf{A}^\mathrm{T} \mathbf{A}$ 总是对称正定的，若 $\mathbf{A} \vec{x} = \vec{b}$ 不是 欠约束的（underconstrained），即 $\mathbf{A}^\mathrm{T} \mathbf{A}$ 非奇异，那么就可以用梯度法或者 CG 求解 $(\textrm{e.q. 47})$ 。也就是说，当 $\mathbf{A}$ 不是对称正定阵的时候，若满足特定的条件，那么也是可以采用梯度法或者 CG 求解的。这就将二者扩展到了更为广泛的应用场景中去了。

CG 也可以拓展到任意连续函数上，而不仅仅局限于二次型。但是要面临许多新的问题：

残差向量 $r_{(i)}$ 不再等于 $\vec{b} - \mathbf{A} \vec{x}_{(i)}$ 。常用的做法是 $\vec{r}_{(i)} \leftarrow -f'(\vec{x}_{(i)})$ ；
最优步长 $\alpha_{(i)}$ 依然通过求导获得，但是更加复杂。一阶导为零 对应的方程需要用到一些数值计算的方法来求解，如牛顿法和割线法等；
$\beta_{(i)}$ 有多重可选的方案。目前常用的有 Fletcher-Reeves 方程（FR）和 Polak-Ribière 方程（PR），其表达式分别如下： $$ \begin{equation} \left\{ \begin{array}{l} \beta_{(i+1)}^{FR} = \frac{\vec{r}_{(i+1)}^\mathrm{T} \vec{r}_{(i+1)}}{\vec{r}_{(i)}^\mathrm{T} \vec{r}_{(i)}} \\ \beta_{(i+1)}^{PR} = \frac{\vec{r}_{(i+1)}^\mathrm{T} (\vec{r}_{(i+1)} - \vec{r}_{(i)})}{\vec{r}_{(i)}^\mathrm{T} \vec{r}_{(i)}} \end{array} \right. \end{equation} $$ FR 就是 $f(\vec{x})$ 为二次型时我们所采用的那个。在起始点足够接近我们想要求解的最小值点的情况下，前者能够收敛，后者在少数情况下却会无限循环而不收敛，但是速度更快。一种解决 PR 不收敛的方案是 $$ \begin{equation} \beta_{(i+1)} \leftarrow \max \bigg \{\frac{\vec{r}_{(i+1)}^\mathrm{T} (\vec{r}_{(i+1)} - \vec{r}_{(i)})}{\vec{r}_{(i)}^\mathrm{T} \vec{r}_{(i)}}, 0\bigg \}, \end{equation} $$ 本质上就是当 $\beta_{(i+1)}^{PR} < 0$ 时开启一轮新的 CG。

非线性 CG 算法几乎没有像线性 CG 算法的收敛性保证。函数 $f$ 和二次型函数越不像，搜索方向失去共轭性的速度就越快。此外， $f$ 可能会存在多个局部最小值点，CG 算法并不保证能收敛到全局最小值点。若 $f$ 没有下界的话，CG 甚至都找不到局部最小值点。

说明

撰写这份文档的初衷是完成《计算机应用数学》课程的最后一次作业。总体上，本文是对 Jonathan Richard Shewchuk 的讲义 An Introduction to the Conjugate Gradient Method Without the Agonizing Pain 的重新演绎，也参考了这篇博客的一些信息，但加入了一些我个人的理解。此外，我删去了很多原文中有些多余的叙述。本文的核心内容是讲解共轭梯度法，但也捎带阐述了梯度法和一些线性代数的理论。本文对共轭梯度的解释是极为充实的，设计原理、算法实现以及收敛性分析均被涵盖在内，希望可以对读者有切实的帮助。

关于共轭梯度法的全部论述（上、下）中出现的图片均来自讲义 An Introduction to the Conjugate Gradient Method Without the Agonizing Pain。

本文档的 pdf 版本可以在《理解共轭梯度法》下载。

致谢

感谢 Licai Chu 教授认真细致地指出本文的各类错误。本文档已于 2021 年 1 月修改。

转载申请

本作品采用知识共享署名 4.0 国际许可协议进行许可，转载时请注明原文链接。您必须给出适当的署名，并标明是否对本文作了修改。