理解共轭梯度法（上）· 梯度法及其分析

求解无约束非线性优化问题的算法有很多种。最常用的无约束非线性优化算法是一维搜索，其核心是找到 合适的迭代方向 以及每次迭代的 最优步长。如果没有曲线信息可供利用（一阶、二阶甚至更高阶的导数），那么可以用黄金分割法、斐波那契法等方法缩小搜索区间，也可以借助多项式的强大表示能力执行插值法（牛顿法就是二点二次插值）；如果有信息可用，那么通常借助泰勒展开式获得迭代方向。具体地，如果有一阶信息可供利用，那么可以采用梯度法（最速下降法）及其一系列的改进方法（泰勒一阶展开）；如果有二阶信息可供利用，那么可以采用牛顿法及其一系列的改进方法（泰勒二阶展开）。牛顿法的两大问题分别是 Hessian 矩阵不总正定和 Hessian 矩阵的逆太难算。对于前者，改进策略是提出各种修正方案保证迭代方向一定是函数下降的方向。共轭梯度法（Conjugate Gradient method, CG）就是一种常用的改进方法，其收敛速度介于梯度法和牛顿法之间；对于后者，改进策略是各种拟牛顿法（用别的矩阵来代替 Hessian 矩阵的逆）。除了一维搜索，另一类无约束非线性优化的算法是信赖域方法。本质上，信赖域方法是在局部用二次型插值目标曲线，仍就是借助多项式的强大表示能力。

本文将重点介绍共轭梯度法（以下简称 CG）。CG 是解决大型线性方程组问题最流行的迭代算法。它对于如下形式的问题特别有效： $$ \begin{equation} \mathbf{A} \vec{x} = \vec{b}, \end{equation} $$ 其中 $\mathbf{A} \in \mathbb{R}^{n \times n}$ 是一个对称正定矩阵 ¹，$\vec{b} \in \mathbb{R}^n$ 是一个已知向量，$\vec{x} \in \mathbb{R}^n$ 是待求解的未知向量。当然，我们有很多算法可以求解线性方程组问题，例如高斯消去法（对 $\mathbf{A}$ 执行 LU 分解）、基于迭代的 Jacobi 方法、Gauss-Seidel 方法以及松弛法等。作为一种基于迭代的方法，和高斯消去法相比，CG 的优势在于当 $\mathbf{A}$ 是大规模稀疏矩阵的时候，其速度和内存占用都小于高斯消去法；和 Jacobi 方法及其改进相比，当 $\mathbf{A}$ 是对称正定矩阵时，CG 可以保证收敛到 $ \mathbf{A} \vec{x} = \vec{b} $ 的真值。这些结论我们都会在后文中给出证明。

本文将从二次型出发，首先给出梯度法及其性能分析，随后深入分析 CG 的理论原理、算法步骤、最优性以及收敛速率。此外，除非明确指出，否则本文提到的矩阵均为 $n$ 阶方阵。

1 二次型

二次型（the Quadratic Form）是一个从向量映射到标量的函数： \begin{equation} f(\vec{x}) \triangleq \frac{1}{2} \vec{x}^\mathrm{T} \mathbf{A} \vec{x} - \vec{b}^\mathrm{T} \vec{x} + c, \end{equation} 其中 $\mathbf{A} \in \mathbb{R}^{n \times n}$，$\vec{x},\vec{b} \in \mathbb{R}^n$，$c \in \mathbb{R}$。根据矩阵微积分可知$\frac{\partial \vec{x}^\mathrm{T} \mathbf{A} \vec{x}}{\partial \vec{x}} = (\mathbf{A} + \mathbf{A}^\mathrm{T}) \vec{x}$，$\frac{\partial \vec{b}^\mathrm{T} \vec{x}}{\partial \vec{x}} = \vec{b}$。当 $\mathbf{A}$ 是一个对称矩阵时，$\frac{\partial \vec{x}^\mathrm{T} \mathbf{A} \vec{x}}{\partial \vec{x}} = 2 \mathbf{A} \vec{x}$，$\nabla_{\vec{x}} f(\vec{x}) = \mathbf{A} \vec{x} - \vec{b}$。

根据 “局部极小值存在的一阶必要条件”，$f(\vec{x})$ 的 局部极小值 由 $\frac{1}{2}(\mathbf{A} + \mathbf{A}^\mathrm{T}) \vec{x} = \vec{b}$ 的解给出。当 $\mathbf{A}$ 是一个对称正定矩阵时，$\mathbf{A}$ 必然可逆 ²，因此不妨设 $\vec{x}^\star = \mathbf{A}^{-1} \vec{b}$，即 $\nabla_{\vec{x}} f(\vec{x}) = 0$ 的解。令 $\vec{x} = \vec{x}^\star + \vec{e}$，则 $\forall \vec{e} \in \mathbb{R}^n$， $$ \begin{aligned} f(\vec{x}^\star + \vec{e}) &= \frac{1}{2} (\vec{x}^\star + \vec{e})^\mathrm{T} \mathbf{A} (\vec{x}^\star + \vec{e}) - \vec{b}^\mathrm{T} (\vec{x}^\star + \vec{e}) + c \\ &= f(\vec{x}^\star) + \frac{1}{2} \vec{e}^\mathrm{T} \mathbf{A} \vec{e} > f(\vec{x}^\star). \end{aligned} $$ 这说明当 $\mathbf{A}$ 是一个对称正定矩阵时，通过求解 $\mathbf{A} \vec{x} = \vec{b}$ 得到的就是 $f(\vec{x})$ 的 全局最小值。这相当于把一个二次型的最优化问题转变成了线性方程组的求解问题。当 $\mathbf{A}$ 是一个对称正定矩阵时，$f(\vec{x})$ 的图像是一个图形开口向上的抛物面。如果 $\mathbf{A}$ 非正定，那么其全局最小值点就可能不止一个。下图展示了不同的 $\mathbf{A} \in \mathbb{R}^{2 \times 2}$ 对 $f(\vec{x})$ 的图像的影响。

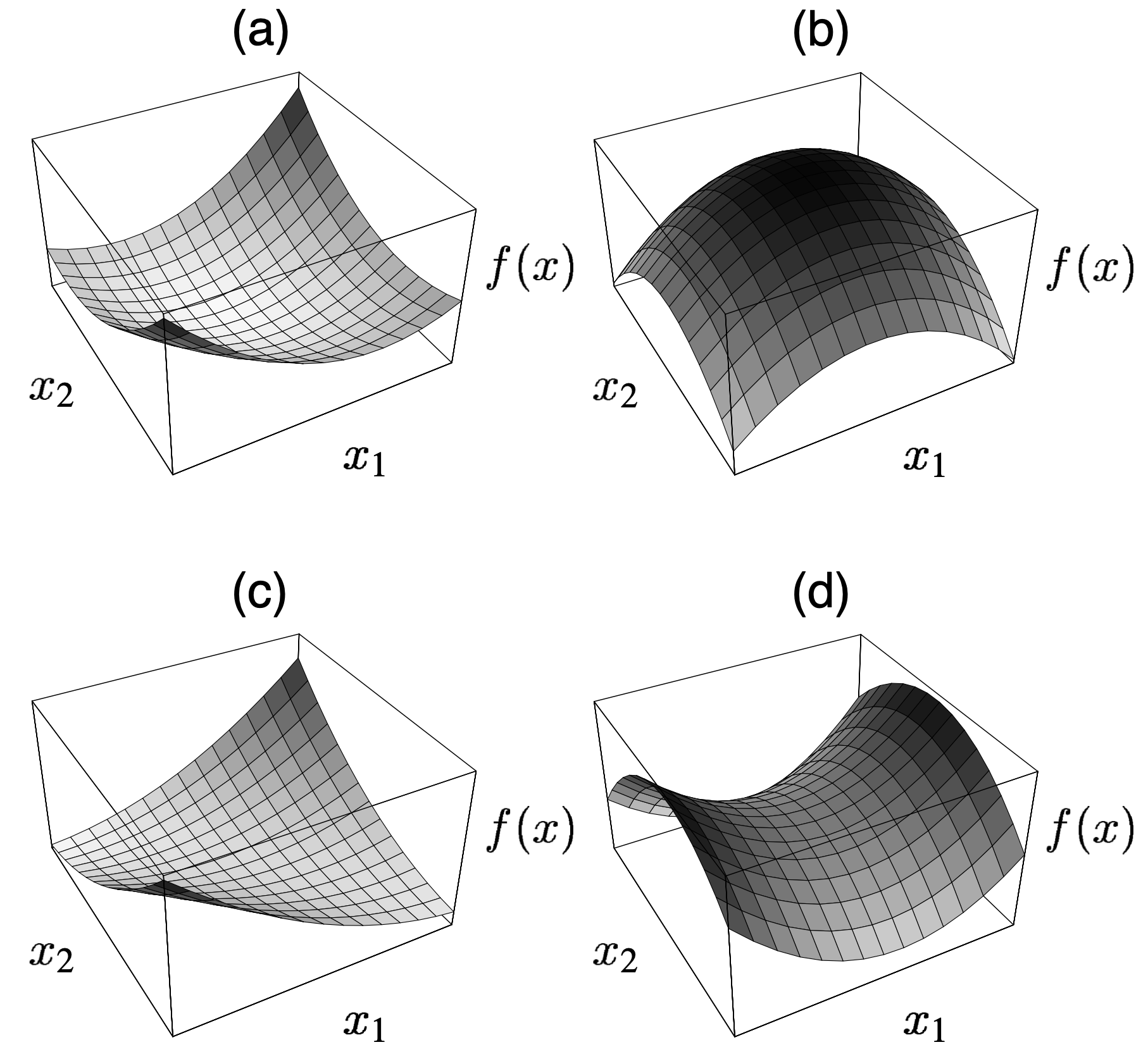
2 最速下降法

2.1 方向和最优步长

最速下降法即梯度法。作为一种一维搜索算法，梯度法采取函数梯度的反方向作为迭代方向，并通过求导的方式确定迭代的最优步长。因为梯度是函数值增长最快的方向，所以梯度下降的方向是函数值减少最快的方向，这就是为什么梯度法又被称为最速下降法的原因。在梯度法中，我们将从任意点 $\vec{x}_{(0)}$ 开始，经过迭代得到 $\vec{x}_{(1)}, \vec{x}_{(2)}, \cdots$，直到达到最大迭代次数或者误差满足要求为止。 在第 $i$ 轮迭代中，梯度法选择的方向为 $\vec{b} - \mathbf{A} \vec{x}_{(i)}$³。 为了简化描述，我们定义如下变量：

• 误差向量：$\vec{e}_{(i)} \triangleq \vec{x}_{(i)} - \vec{x}^\star$，表示第 $i$ 和全局最小值点 $\vec{x}^\star$ 的距离；
• 残差向量：$\vec{r}_{(i)} \triangleq \vec{b} - \mathbf{A} \vec{x}_{(i)}$，表示第 $i$ 轮迭代时 $\mathbf{A} \vec{x}_{(i)}$ 和 $\vec{b}$ 之间的距离。

残差向量其实就是最速下降的方向， 且 $\vec{r}_{(i)} = \vec{b} - \mathbf{A} \vec{x}_{(i)} = \mathbf{A} \vec{x}^\star - \mathbf{A} \vec{x}_{(i)} = -\mathbf{A} \vec{e}_{(i)}$。 这个等价变换会反复用到，务必记住。因此 $\vec{x}$ 将按照如下公式进行更新： $$ \begin{equation} \vec{x}_{(i+1)} \leftarrow \vec{x}_{(i)} + \alpha \cdot \vec{r}_{(i)}, \end{equation} \tag{e.q. 1} $$ 其中 $\alpha$ 是第 $i$ 轮迭代时的 最优步长。如何确定 $\alpha$ 呢？如果我们将 $f(\vec{x}_{(i+1)})$ 视为 $\alpha$ 的函数 $\varphi(\alpha)$， 那么根据 局部极小值存在的一阶必要条件，$\alpha$ 应当使得 $\nabla_{\alpha} \varphi(\alpha) = 0$，即 $$ \begin{equation} \begin{aligned} \nabla_{\alpha} \varphi(\alpha) &= \nabla_{\alpha} f(\vec{x}_{(i+1)})\\ &= \big(\nabla_{\vec{x}_{(i+1)}} f(\vec{x}_{(i+1)})\big)^\mathrm{T} \nabla_{\alpha} \vec{x}_{(i+1)} \\ &= - \vec{r}_{(i+1)}^\mathrm{T} \vec{r}_{(i)} \\ &= 0. \end{aligned} \end{equation} \tag{e.q. 2} $$ $(\textrm{e.q. } 2)$ 表明最优步长 $\alpha$ 使得前后两轮的迭代方向相互垂直（正交）。关于 $\alpha$ 的确定，图 2 给了一个形象的描述。

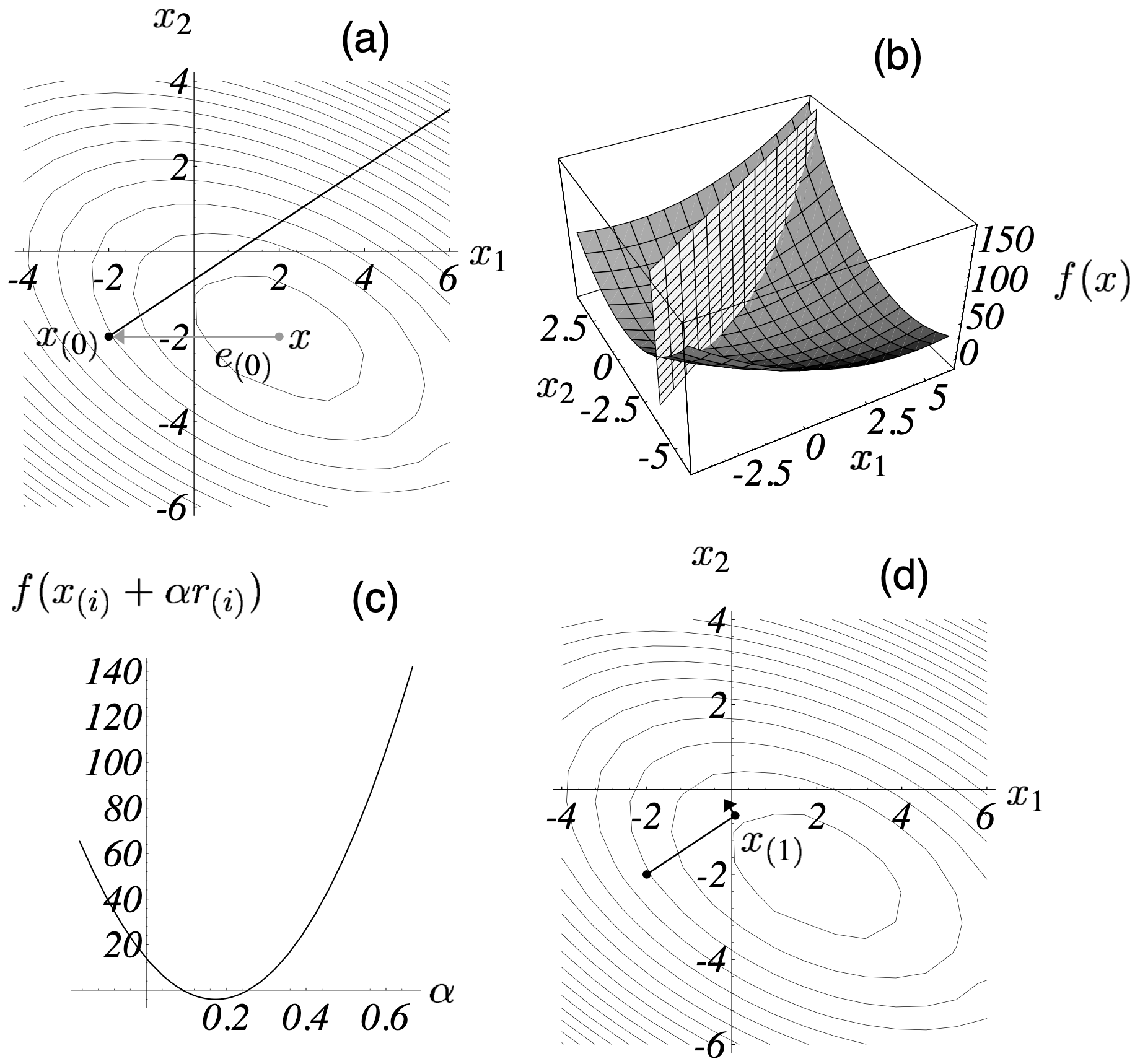
根据 $(\textrm{e.q. } 2)$ 可得：

$$ \begin{equation} \begin{split} \vec{r}_{(i+1)}^\mathrm{T} \vec{r}_{(i)} &= (\vec{b} - \mathbf{A} \vec{x}_{(i+1)})^\mathrm{T} \vec{r}_{(i)} \\ &= \big[\vec{b} - \mathbf{A} (\vec{x}_{(i)} + \alpha \cdot \vec{r}_{(i)}) \big]^\mathrm{T} \vec{r}_{(i)} \\ &= (\vec{b} - \mathbf{A} \vec{x}_{(i)})^\mathrm{T} \vec{r}_{(i)} - \alpha (\mathbf{A}\vec{r}_{(i)})^\mathrm{T} \vec{r}_{(i)} \\ &= \vec{r}_{(i)}^\mathrm{T} \vec{r}_{(i)} - \alpha \vec{r}_{(i)}^\mathrm{T} \mathbf{A} \vec{r}_{(i)} \\ &= 0, \end{split} \tag{e.q. 3} \end{equation} $$

因此可以确定 $\alpha$ 的取值： $$ \begin{equation} \alpha = \frac{\vec{r}_{(i)}^\mathrm{T} \vec{r}_{(i)}}{\vec{r}_{(i)}^\mathrm{T} \mathbf{A} \vec{r}_{(i)}}. \tag{e.q. 4} \end{equation} $$ 至此，梯度法已经讲解完毕。其过程为：对于任意初始点 $\vec{x}_{(0)}$，将 $(\textrm{e.q. } 4)$ 代入 $(\textrm{e.q. } 1)$ 中，根据 $(\textrm{e.q. } 1)$ 更新依次得到 $\vec{x}_{(1)}, \vec{x}_{(2)}, \cdots$，直到达到最大迭代次数或者误差满足要求为止。当 $\mathbf{A}$ 为对称正定阵的时候，梯度法一定可以收敛到全局最优解，因此迭代的终止条件可设为 $\vec{r}_k = \vec{0}$。梯度法的算法描述在 算法 1 中。

算法 1 的每一轮迭代中有两次矩阵 - 向量乘法运算（step 5 和 step 7），这是很耗时的。因此，我们可以想办法减少一次矩阵 - 向量乘法来降低复杂度。怎么操作？观察 算法 1 第 6 行，有

$$ \begin{equation} \begin{split} \vec{x}_{(k)} &= \vec{x}_{(k-1)} + \alpha_{(k)} \cdot \vec{r}_{(k-1)} \quad \Longleftrightarrow \\ - \mathbf{A} \vec{x}_{(k)} + \vec{b} &= - (\mathbf{A} \vec{x}_{(k-1)} - \vec{b}) - \alpha_{(k)} \mathbf{A} \vec{r}_{(k-1)} \quad \Longleftrightarrow \\ \vec{r}_{(k)} &= \vec{r}_{(k-1)} - \alpha_{(k)} \mathbf{A} \vec{r}_{(k-1)}. \end{split} \tag{e.q. 5} \end{equation} $$

$(\textrm{e.q. 5})$ 表明我们可以用 $\vec{r}_{(k-1)} - \alpha_{(k)} \mathbf{A} \vec{r}_{(k-1)}$ 代替 $\vec{b} - \mathbf{A} \vec{x}_{(k)}$ 来更新 $\vec{r}_{(k)}$！ 因为 $\mathbf{A} \vec{r}_{(k-1)}$ 的结果可以复用，所以这就避免了第 7 行的矩阵 - 向量乘法。但是，有得必有失。这种降低复杂度的策略是以牺牲计算 $\vec{r}_{(k)}$ 的精度为代价的。因为 $\vec{r}_{(k)}$ 的计算没有用到最新的 $\vec{x}_{(k)}$， 所以会有 舍入误差。这个问题可以通过定期重新采用 $\vec{b} - \mathbf{A} \vec{x}_{(k)}$ 更新 $\vec{r}_{(k)}$ 解决。改进策略的算法描述在 算法 2 中。

2.2 特征值的相关特性

2.2.1 谱半径

求解线性方程组的迭代算法通常会反复将一个矩阵作用在一个向量上。因此本章节先谈一谈特征值和特征向量的相关特性，再开展梯度法的收敛性分析。

设 $\vec{v}$ 是矩阵 $\mathbf{B}$ 的一个特征向量，则存在常数 $\lambda$ 使得 $\mathbf{B} \vec{v} = \lambda \vec{v}$。也就是说，当 $\mathbf{B}$ 作为一个线性变换作用到向量 $\vec{v}$ 上时， 只会让 $\vec{v}$ 在所在方向上发生长度的伸缩或变成反向向量，而不会发生旋转变换。不断地左乘 $\mathbf{B}$，我们主要关心如下两种不同的情形：

• 若 $| \lambda | <1$，那么 $\lim_{k \to \infty} \mathbf{B}^k \vec{v}$ 会收缩至 $0$；
• 若 $| \lambda | > 1$，那么 $\lim_{k \to \infty} \mathbf{B}^k \vec{v}$ 会趋于 $\infty$。

图 3 和图 4 分别给出了一个对应的例子。

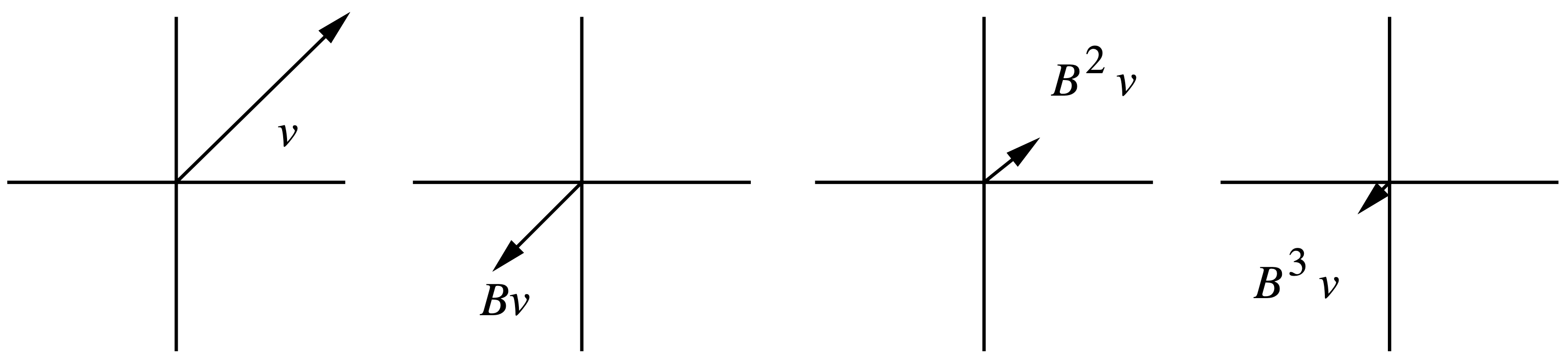
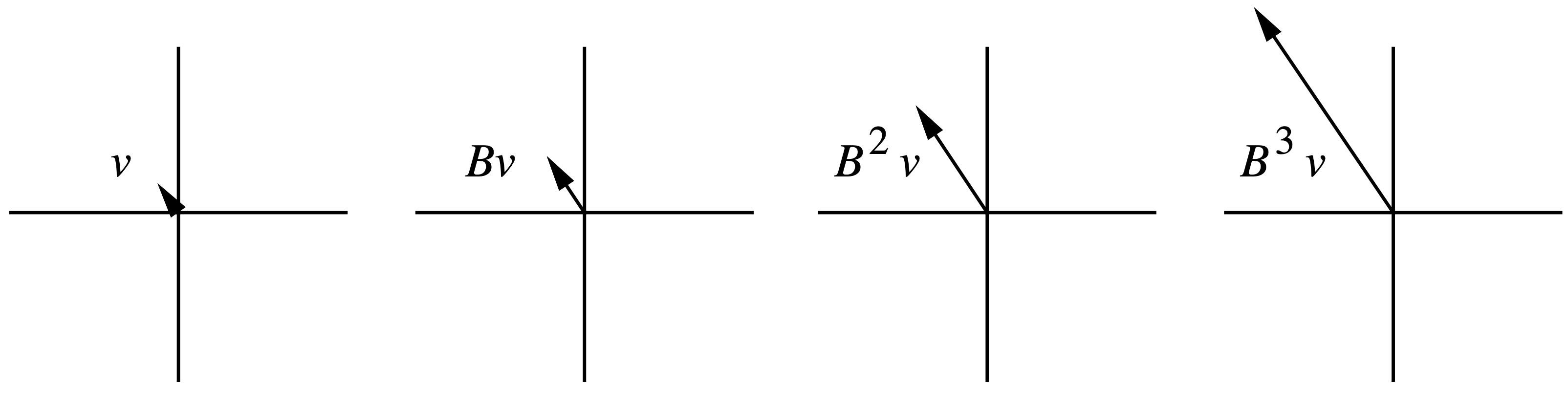
如果将向量看成线性空间中的一个点，那么左乘矩阵可以看成是对点施加的一种运动（使点发生位移）。特征值反映了运动的速度，而特征向量则反映了运动的方向。线性变换是各个方向上不同速度的运动的叠加。从这个理解出发，就会想明白为什么对于任意向量 $\vec{x}$，不断左乘 $\mathbf{B}$，$\vec{x}$ 会不断贴合到 $\mathbf{B}$ 最大特征值对应的特征空间上。我们知道，特征值分解就是和对角阵互为相似矩阵，即对角化。任意矩阵 $\mathbf{B} \in \mathbb{R}^{n \times n}$ 可对角化当且仅当该矩阵具有 $n$ 个线性无关的特征向量 ⁴。任意对称矩阵都可以进行正交对角化，即其 $n$ 个线性无关的特征向量组成的矩阵是一个正交矩阵。当我们将对称阵 $\mathbf{B}$ 作用在任意向量 $\vec{x}$ 上时，可以将 $\vec{x}$ 用 $\mathbf{B}$ 的 $n$ 个线性无关的特征向量 $\{\vec{v}_1, ..., \vec{v}_n\}$ 的线性组合表示，即 $$ \begin{aligned} \vec{x} = \sum_{i = 1}^n c_i \vec{v}_i, \end{aligned} $$ 那么 $\mathbf{B} \vec{x} = \sum_{i=1}^n c_i \lambda_i \vec{v}_i$，其中 $\lambda_i$ 为 $\vec{v}_i$ 对应的特征值。注意，我们总可以选取合适的特征向量使得 $\forall i, c_i = 1$。因此上式可简化为 $\vec{x} = \sum_{i = 1}^n \vec{v}_i$。那么，只要存在一个 $i$ 使得 $|\lambda_i| > 1$，$\mathbf{B}^k \vec{x}$ 的长度就会发散至无穷大。只有当所有特征值的绝对值均小于 1 时，$\mathbf{B}^k \vec{x}$ 才能收敛到 $\vec{0}$。可以看出，$\mathbf{B}^k \vec{x}$ 能否收敛到 $\vec{0}$ 是由最大的 $|\lambda_i|$ 决定的，我们将这个数值定义为 $\mathbf{B}$ 的 谱半径（spectral radius）： $$ \begin{equation} \rho(\mathbf{B}) \triangleq \max_{i} |\lambda_i|. \end{equation} $$ 如果 $\mathbf{B}$ 不具备 $n$ 个线性无关的特征向量，那么我们称 $\mathbf{B}$ 是 退化矩阵（defective matrix）。此时无法对角化（特征值分解）。本文只关心对称正定阵，因此关于退化矩阵的内容不再展开描述。

2.2.2 雅各比迭代

我们先前提到过，对于线性方程组问题 $\mathbf{A} \vec{x} = \vec{b}$，一类典型的方法是 Jacobi 算法。Gauss-Seidel 方法和松弛法均是在 Jacobi 算法的基础上的改进版本。本章节我们将深入理解 Jacobi 算法，其中涉及的一些观念将会用于梯度法的收敛性分析。

将 $\mathbf{A} \vec{x} = \vec{b}$ 展开可得 $$ \begin{equation} x_i = \frac{b_i - \sum_{j \neq i} a_{ij}x_j}{a_{ii}}, \end{equation} $$ 由此可得 Jacobi 的迭代公式： $$ \begin{equation} x_i^{(k+1)} = \frac{b_i - \sum_{j=1}^{i-1}a_{ij}x_j^{(k)} - \sum_{j=i+1}^n a_{ij}x_j^{(k)}}{a_{ii}} \tag{e.q. 6} \end{equation} $$ 显然该方法要求 $\forall i, a_{ii} \neq 0$。如果在更新 $x_i^{(k+1)}$ 的时候对于所有排在其前面的 $x_j$ 采用最新的数据 $x_j^{(k+1)}$，那么就得到了 $$ \begin{equation} x_i^{(k+1)} = \frac{b_i - \sum_{j=1}^{i-1}a_{ij}x_j^{(k+1)} - \sum_{j=i+1}^n a_{ij}x_j^{(k)}}{a_{ii}}, \end{equation} $$ 这就是 Gauss-Seidel 方法的迭代公式。不出意外地，Gauss-Seidel 方法的收敛速度应当快于 Jacobi 方法。

我们也可以采用矩阵分解的方式表达上述迭代方程。具体地，令 $\mathbf{D} = \textrm{diag}(\mathbf{A})$，$\mathbf{E}$ 是 $\mathbf{A}$ 严格下三角部分的负组成的下三角矩阵，$\mathbf{F}$ 是 $\mathbf{A}$ 严格上三角部分的负组成的上三角矩阵，则 $\mathbf{A} = \mathbf{D} - \mathbf{E} - \mathbf{F}$。所以 $\mathbf{A} \vec{x} = \vec{b}$ 等价于 $$ \begin{aligned} (\mathbf{D} - \mathbf{E} - \mathbf{F}) \vec{x} &= \vec{b} \\ \mathbf{D}^{-1} (\mathbf{D} - \mathbf{E} - \mathbf{F}) \vec{x} &= \mathbf{D}^{-1} \vec{b} \\ \vec{x} &= \mathbf{D}^{-1} (\mathbf{E} + \mathbf{F}) \vec{x} + \mathbf{D}^{-1} \vec{b}. \end{aligned} $$ 定义 $\mathbf{B} \triangleq \mathbf{D}^{-1} (\mathbf{E} + \mathbf{F})$，$\vec{z} \triangleq \mathbf{D}^{-1} \vec{b}$，则 Jacobi 迭代公式 $(\textrm{e.q. 6})$ 可写作 $$ \begin{equation} \vec{x}_{(k+1)} = \mathbf{B} \vec{x}_{(k)} + \vec{z}. \tag{e.q. 7} \end{equation} $$ 我们将 $\mathbf{A} \vec{x} = \vec{b}$ 的真值记为 $\vec{x}^\star$，并称之为驻点（stationary point）。第 $i$ 轮迭代中的 $\vec{x}_{(i)}$ 可以用真值 $\vec{x}^\star$ 和误差向量 $\vec{e}_{(i)}$ 之和来表示，那么根据 $(\textrm{e.q. 7})$ 可得 $$ \begin{align} \vec{x}_{(i+1)} &= \mathbf{B} \vec{x}_{(i)} + \vec{z} \\ &= \mathbf{B} (\vec{x}^\star + \vec{e}_{(i)}) + \vec{z} \\ &= \mathbf{B} \vec{x}^\star + \vec{z} + \mathbf{B} \vec{e}_{(i)} \\ &= \vec{x}^\star + \mathbf{B} \vec{e}_{(i)}，&& \vec{x}^\star = \mathbf{B} \vec{x}^\star + \vec{z} \textrm{ always holds} \end{align} $$ 所以 $\vec{e}_{(i+1)} = \vec{x}_{(i+1)} - \vec{x}^\star = \mathbf{B} \vec{e}_{(i)}$。这表明 Jacobi 方法是通过不断减小误差项来向真值逼近的。若 $\rho(\mathbf{B}) < 1$，则误差项可以收敛到 $\vec{0}$，Jacobi 方法可以解出 $\vec{x}^\star$。同时我们也可以发现，初始向量 $\vec{x}_{(0)}$ 虽然不影响最终的结果，但却会影响到收敛到给定误差范围内需要迭代的次数。Jacobi 的方法的劣势在于：$\mathbf{B}$ 并不总是对称阵，甚至可能是退化矩阵，因此 Jacobi 方法并非对于所有的 $\mathbf{A}$ 都能收敛，即使 $\mathbf{A}$ 是正定矩阵也无法保证收敛。

2.3 收敛性分析

2.3.1 简单情形

为了分析梯度法的收敛速度，我们首先考虑一种简单的情形，即误差向量 $\vec{e}_{(i)}$ 是 $\mathbf{A}$ 的特征值 $\lambda_{e}$ 所对应的特征向量。那么残差向量 $\vec{r}_{(i)} = - \mathbf{A} \vec{e}_{(i)} = - \lambda_e \vec{e}_{(i)}$。 显然 $$ \begin{equation} \mathbf{A} \vec{r}_{(i)} = -\lambda_e \mathbf{A} \vec{e}_{(i)} = \lambda_e \vec{r}_{(i)}, \tag{e.q. 8} \end{equation} $$ 所以 $\vec{r}_{(i)}$ 也是 $\mathbf{A}$ 的特征值 $\lambda_{e}$ 所对应的特征向量。

根据 $(\textrm{e.q. } 4)$ 可得最优步长 $\alpha$ 满足 $$ \begin{equation} \begin{split} \alpha &= \frac{\vec{r}_{(i)}^\mathrm{T} \vec{r}_{(i)}}{\vec{r}_{(i)}^\mathrm{T} \mathbf{A} \vec{r}_{(i)}} = \frac{\vec{r}_{(i)}^\mathrm{T} \vec{r}_{(i)}}{\vec{r}_{(i)}^\mathrm{T} \lambda_e \vec{r}_{(i)}} \qquad \vartriangleright \textrm{(e.q. 8)} \\ &= \frac{\vec{r}_{(i)}^\mathrm{T} \vec{r}_{(i)}}{\lambda_e \vec{r}_{(i)}^\mathrm{T} \vec{r}_{(i)}} = \frac{1}{\lambda_e}. \end{split} \tag{e.q. 9} \end{equation} $$ 又由 $(\textrm{e.q. } 1)$ 可得 $\vec{e}_{(i+1)} + \vec{x}^\star = \vec{e}_{(i)} + \vec{x}^\star + \alpha \cdot \vec{r}_{(i)}$, 因此 $$ \begin{equation} \vec{e}_{(i+1)} = \vec{e}_{(i)} + \alpha \cdot \vec{r}_{(i)}. \tag{e.q. 10} \end{equation} $$ 从而 $$ \begin{aligned} \vec{e}_{(i+1)} &= \vec{e}_{(i)} + \frac{1}{\lambda_e}\vec{r}_{(i)} \qquad \vartriangleright \textrm{(e.q. 9)} \\ &= \vec{e}_{(i)} - \frac{1}{\lambda_e} \lambda_e \vec{e}_{(i)} \\ &= \vec{0}. \end{aligned} $$ 这说明在该条件下梯度法只需要一次迭代即可抵达 $\vec{x}^\star$！图 5 对该结论给出了一个形象的解释。

当误差向量 $\vec{e}_{(i)}$ 不是 $\mathbf{A}$ 的特征值 $\lambda_{e}$ 所对应的特征向量时，梯度法的收敛性又如何呢？假设 $\mathbf{A}$ 是对称阵，则 $\mathbf{A}$ 可进行正交对角化： $$ \begin{equation} \mathbf{A} = \mathbf{P} \mathbf{D} \mathbf{P}^{-1} = \mathbf{P} \mathbf{D} \mathbf{P}^\mathrm{T}, \end{equation} $$ 其中 $\mathbf{P} = \{\vec{v}_1, ..., \vec{v}_n\}$ 的每一列是相互单位正交的特征向量（显然 $ \{\vec{v}_1, ..., \vec{v}_n\}$ 线性无关），$\mathbf{D} = \textrm{diag}(\lambda_1, ..., \lambda_n)$ 是一个由 $n$ 个实特征值（包含重根）组成的对角阵。不妨将误差向量 $\vec{e}_{(i)}$ 用特征向量的线性组合表示： $$ \begin{equation} \vec{e}_{(i)} = \sum_{i=1}^n \xi_i \vec{v}_i, \tag{e.q. 11} \end{equation} $$ 则 $\Vert \vec{e}_{(i)} \Vert^2 = \sum_{i=1}^n \xi^2$，且 $\vec{r}_{(i)} = - \mathbf{A} \vec{e}_{(i)} = - \sum_{i=1}^n \xi_i \lambda_i \vec{v}_i$，这表明残差向量也可以表达为特征向量的线性组合。 所以 $$ \begin{equation} \vec{e}_{(i)}^\mathrm{T} \mathbf{A} \vec{e}_{(i)} = \big( \sum_{i=1}^n \xi_i \vec{v}_i^\mathrm{T} \big) \big( \sum_{i=1}^n \xi_i \lambda_i \vec{v}_i \big) = \sum_{i=1}^n \xi_i^2 \lambda_i, \tag{e.q. 12} \end{equation} $$

$$ \begin{equation} \begin{split} \vec{r}_{(i)}^\mathrm{T} \mathbf{A} \vec{r}_{(i)} &= \big(\sum_{i=1}^n \xi_i \lambda_i \vec{v}_i^\mathrm{T} \big) \mathbf{A} \big(\sum_{i=1}^n \xi_i \lambda_i \vec{v}_i^\mathrm{T} \big) = \big(\sum_{i=1}^n \xi_i \lambda_i \vec{v}_i \big) \big(\sum_{i=1}^n \xi_i \lambda_i^2 \vec{v}_i \big) = \sum_{i=1}^n \xi_i^2 \lambda_i^3. \end{split} \tag{e.q. 13} \end{equation} $$

由 $\vec{e}_{(i+1)} = \vec{e}_{(i)} + \alpha \cdot \vec{r}_{(i)}$ 可得 $$ \begin{equation} \begin{split} \vec{e}_{(i+1)} &= \vec{e}_{(i)} + \frac{\vec{r}_{(i)}^\mathrm{T} \vec{r}_{(i)}}{\vec{r}_{(i)}^\mathrm{T} \mathbf{A} \vec{r}_{(i)}} \vec{r}_{(i)} \\ &= \vec{e}_{(i)} + \frac{\sum_{i=1}^n \xi_i^2 \lambda_i^2}{\sum_{i=1}^n \xi_i^2 \lambda_i^3} \vec{r}_{(i)} \end{split} \tag{e.q. 14} \end{equation} $$ 请注意，到目前为止所推导出的结论均是基于 “$\mathbf{A}$ 是对称阵” 这一假设的。若所有特征向量的特征值均相同且为 $\lambda$，则 $(\textrm{e.q. 14})$ 变成了 $$ \begin{equation} \begin{split} \vec{e}_{(i+1)} &= \vec{e}_{(i)} + \frac{\lambda^2 \sum_{i=1}^n \xi_i^2}{\lambda^3 \sum_{i=1}^n \xi_i^2} (-\mathbf{A} \vec{e}_{(i)}) \\ &= \vec{e}_{(i)} + \frac{\lambda^2 \sum_{i=1}^n \xi_i^2}{\lambda^3 \sum_{i=1}^n \xi_i^2} (- \lambda \vec{e}_{(i)}) \\ &= \vec{0}. \end{split} \end{equation} $$ 上述推导用到了 $\mathbf{A} \vec{e}_{(i)} = \mathbf{A} \sum_{i=1}^n \xi_i \vec{v}_i = \sum_{i=1}^n \xi_i \mathbf{A} \vec{v}_i = \sum_{i=1}^n \xi_i \lambda \vec{v}_i = \lambda \vec{e}_{(i)}$。 这意味着 当 $\mathbf{A}$ 为对称阵且所有特征值相同时，梯度法依然可以做到一步迭代即收敛。 本质上，这是因为 $f(\vec{x})$ 从椭球体的表面变成了球体的表面，任意点的梯度都经过球心。

让我们来总结一下本章节得出的结论：

• 对于任意 $n$ 阶方阵 $\mathbf{A}$，若误差向量 $\vec{e}_{(i)}$ 是 $\mathbf{A}$ 的特征值 $\lambda_{e}$ 所对应的特征向量，那么梯度法一步迭代即收敛；
• 若 $\mathbf{A}$ 是对称阵且所有特征值相同，则梯度法依然可以做到一步迭代即收敛。

2.3.2 一般情形

当误差向量为任意向量，而此时又存在多个不相等的非零特征值时，梯度法的收敛性如何分析呢？为了解决这个问题，我们需要定义误差向量的 “能量范数”（energy norm）： $$ \begin{equation} \Vert \vec{e} \Vert_{\mathbf{A}} \triangleq (\vec{e}^\mathrm{T} \mathbf{A} \vec{e})^{\frac{1}{2}} \end{equation} $$ 从图 6 可以看出，从点 $\vec{x}^\star$ 出发的两个向量如果能量范数相同，那么它们的终点在 $f(\vec{x})$ 的同一条等势线上。

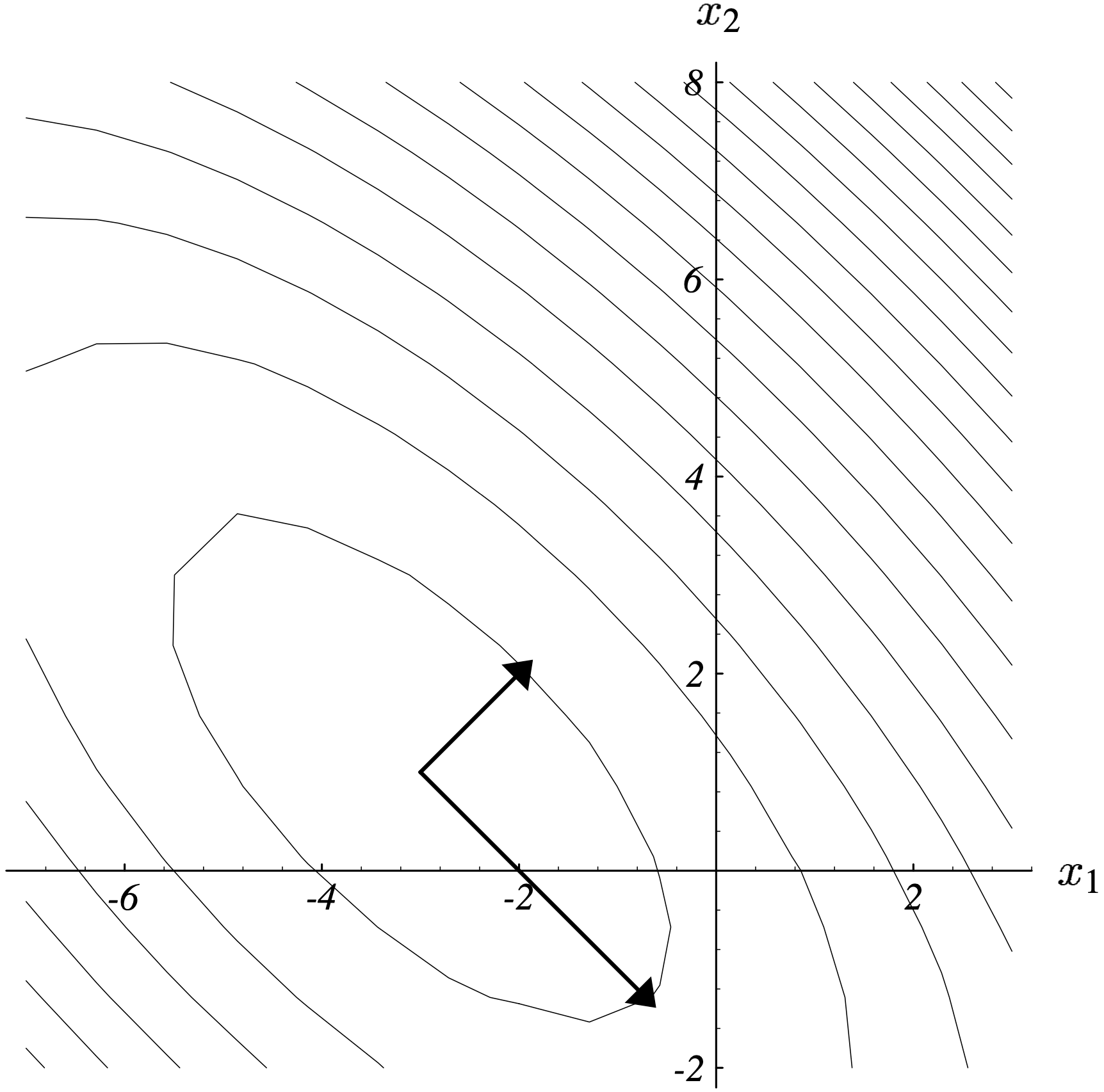
根据能量范数的定义可得 $$ \begin{equation} \begin{split} \Vert \vec{e}_{(i+1)} \Vert_{\mathbf{A}}^2 &= \vec{e}_{(i+1)}^\mathrm{T} \mathbf{A} \vec{e}_{(i+1)} \qquad \vartriangleright \textrm{(e.q. 10)} \\ &= (\vec{e}_{(i)}^\mathrm{T} + \alpha \cdot \vec{r}_{(i)}^\mathrm{T}) \mathbf{A} (\vec{e}_{(i)} + \alpha \cdot \vec{r}_{(i)}) \\ &= \vec{e}_{(i)}^\mathrm{T} \mathbf{A} \vec{e}_{(i)} + 2 \alpha \vec{r}_{(i)}^\mathrm{T} \mathbf{A} \vec{e}_{(i)} + \alpha^2 \vec{r}_{(i)}^\mathrm{T} \mathbf{A} \vec{r}_{(i)} \\ &= \Vert \vec{e}_{(i)} \Vert_{\mathbf{A}}^2 + 2 \frac{\vec{r}_{(i)}^\mathrm{T} \vec{r}_{(i)}}{\vec{r}_{(i)}^\mathrm{T} \mathbf{A} \vec{r}_{(i)}} \big( - \vec{r}_{(i)}^\mathrm{T} \vec{r}_{(i)} \big) + \Big(\frac{\vec{r}_{(i)}^\mathrm{T} \vec{r}_{(i)}}{\vec{r}_{(i)}^\mathrm{T} \mathbf{A} \vec{r}_{(i)}} \Big)^2 \vec{r}_{(i)}^\mathrm{T} \mathbf{A} \vec{r}_{(i)} \vartriangleright \textrm{(e.q. 4)} \\ &= \Vert \vec{e}_{(i)} \Vert_{\mathbf{A}}^2 - \frac{ (\vec{r}_{(i)}^\mathrm{T} \vec{r}_{(i)})^2 }{\vec{r}_{(i)}^\mathrm{T} \mathbf{A} \vec{r}_{(i)}} \\ &= \Vert \vec{e}_{(i)} \Vert_{\mathbf{A}}^2 \bigg( 1 - \frac{(\vec{r}_{(i)}^\mathrm{T} \vec{r}_{(i)})^2}{(\vec{r}_{(i)}^\mathrm{T} \mathbf{A} \vec{r}_{(i)}) (\vec{e}_{(i)}^\mathrm{T} \mathbf{A} \vec{e}_{(i)})} \bigg) \\ &= \Vert \vec{e}_{(i)} \Vert_{\mathbf{A}}^2 \bigg( 1 - \frac{(\sum_{i=1}^n \xi_i^2 \lambda_i^2)^2}{(\sum_{i=1}^n \xi_i^2 \lambda_i) (\sum_{i=1}^n \xi_i^2 \lambda_i^3)} \bigg) \qquad \vartriangleright \textrm{(e.q. 12) & (e.q. 13)} \\ &= \Vert \vec{e}_{(i)} \Vert_{\mathbf{A}}^2 \omega^2 \qquad \vartriangleright \omega^2 \triangleq 1 - \frac{(\sum_{i=1}^n \xi_i^2 \lambda_i^2)^2}{(\sum_{i=1}^n \xi_i^2 \lambda_i) (\sum_{i=1}^n \xi_i^2 \lambda_i^3)} \end{split} \tag{e.q. 15} \end{equation} $$ 我们只要分析 $\omega^2$ 的上界，就可以知道梯度法在最坏情况下的表现了。$\omega$ 越小，收敛速度越快。至于原因，此处暂时按下不表，后文会给出解释。 我们先针对一个简单的情况来分析——$\mathbf{A} \in \mathbb{R}^{2 \times 2}$ 是个正定对称阵进行分析。前文已经说明说明过， 当 $\mathbf{A}$ 是正定矩阵时，其特征值 $\lambda_1,\lambda_2$ 均为正数，且特征向量 $\vec{v}_1, \vec{v}_2$ 线性无关。因此不妨设 $\lambda_1 > \lambda_2$， 此时 $\mathbf{A}$ 的 “谱条件数”（spectral condition number）$\kappa = \lambda_1 / \lambda_2 \geq 1$。请回顾 $(\textrm{e.q. 11})$ ⁵，我们将 误差向量 $\vec{e}_{(i)}$ 相对于特征向量张成的空间 / 坐标系的斜率 定义为 $\mu \triangleq \xi_2 / \xi_1$，由此可对 $\omega^2$ 作如下化简： $$ \begin{equation} \begin{split} \omega^2 &= 1 - \frac{\bigg( \frac{\xi_1^2 \lambda_1^2 + \xi_2^2 \lambda_2^2}{\xi_1^2 \lambda_2^2} \bigg)^2}{\bigg( \frac{\sum_{i=1}^2 \xi_i^2 \lambda_i}{\xi_1^2 \lambda_2} \bigg) \bigg(\frac{\sum_{i=1}^2 \xi_i^2 \lambda_i^3}{\xi_1^2 \lambda_2^3} \bigg)} \\ &= 1 - \frac{(\kappa^2 + \mu^2)^2}{(\kappa + \mu^2) (\kappa^3 + \mu^2)}. \end{split} \tag{e.q. 16} \end{equation} $$ 上式表明我们可以将 $\omega$ 看成 $\kappa$ 和 $\mu$ 的函数（只考虑正数部分）。观察图 7 左图可发现 $\kappa$ 和 $\mu$ 越小，$\omega$ 越小。此外，$\mu = \pm \kappa$ 时 $\omega$ 最大（这个结论从图像上看很直观，也可以通过对 $(\textrm{e.q. 16})$ 求导得到）。分析这个图像也可以理解梯度法是如何做到一步迭代即收敛的。当 $\vec{e}_{(i)}$ 是一个特征向量时，此时误差向量在特征向量组成的坐标系的坐标轴上，因此斜率 $\mu$ 为 $0$ 或 $\infty$，此时均有 $\omega=0$；当 $\mathbf{A}$ 的所有特征值均相等时， $\kappa = 1$，同样有 $\omega=0$。此外，我们可以观察一下 $\omega$ 随 $\kappa$ 和 $\mu$ 的变化情况。当 $\kappa$ 很小的时候，不论 $\mu$ 如何，不论初始点如何选取，收敛速度都是比较快的， 这是因为 $\mathbf{A}$ 各个方向的特征值相似，所以 $f(\vec{x})$ 接近球形，在各个点处均有合适的迭代方向；当 $\kappa$ 很大的时候，不同的特征向量的能量范数差距很大， 此时 $f(\vec{x})$ 的一极相对另一极长很多（想象一个 $a$ 和 $b$ 差异很大的椭圆 $x^2/a^2 + y^2/b^2 = 1$）。如果初始点在山脊处，那么迭代方向还是很好找的，收敛速度不算慢；如果初始点在山谷处， 那么梯度法只能朝着波谷方向曲折而缓慢的前进，每一步迭代作出的有效改进很小，收敛速度很慢。图 7 右图给四种情形下梯度法的迭代情况做了一个形象化的展示。

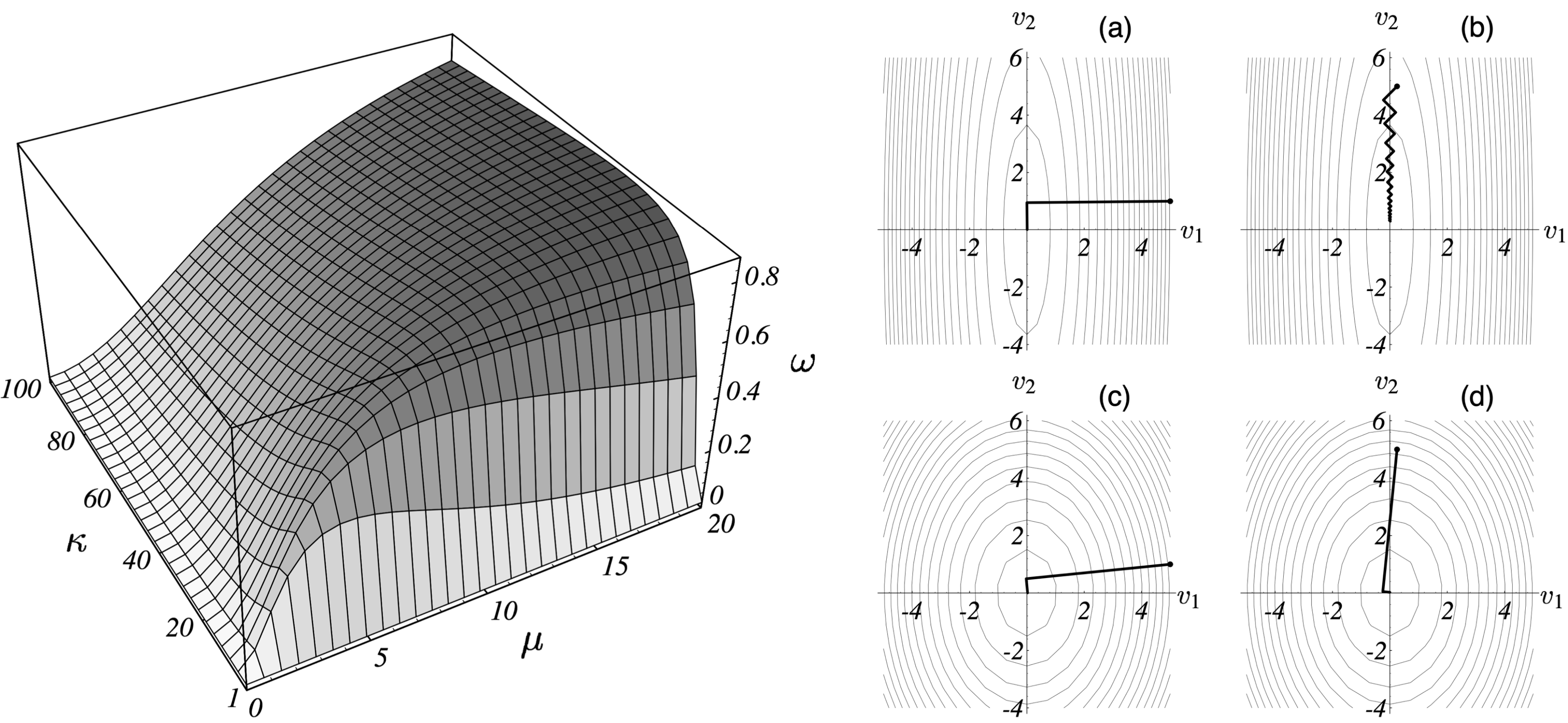
我们再来算一算最差的情况下，即 $\mu = \pm \kappa$ 时 $\omega$ 的上界是多少。 对于对称正定阵 $\mathbf{A}$，我们将 “条件数”（condition number）定义为特征值之比的最大值： $$ \begin{equation} \kappa \triangleq \frac{\lambda_{max}}{\lambda_{min}}. \end{equation} $$ 当 $\mu = \pm \kappa$ 时有 $\mu^2 = \kappa^2$，因此 $\textrm{(e.q. 16)}$ 满足 $$ \omega^2 \leq 1 - \frac{4\kappa^4}{\kappa^5 + 2\kappa^4 + \kappa^3} \leq \Big( \frac{\kappa-1}{\kappa+1} \Big)^2, $$ 进而得到 $$ \begin{equation} \omega \leq \frac{\kappa-1}{\kappa+1}. \tag{e.q. 17} \end{equation} $$ 该结论在 $n \geq 2$ 时依然成立。将 $(\textrm{e.q. 17})$ 绘制出来可得下图：

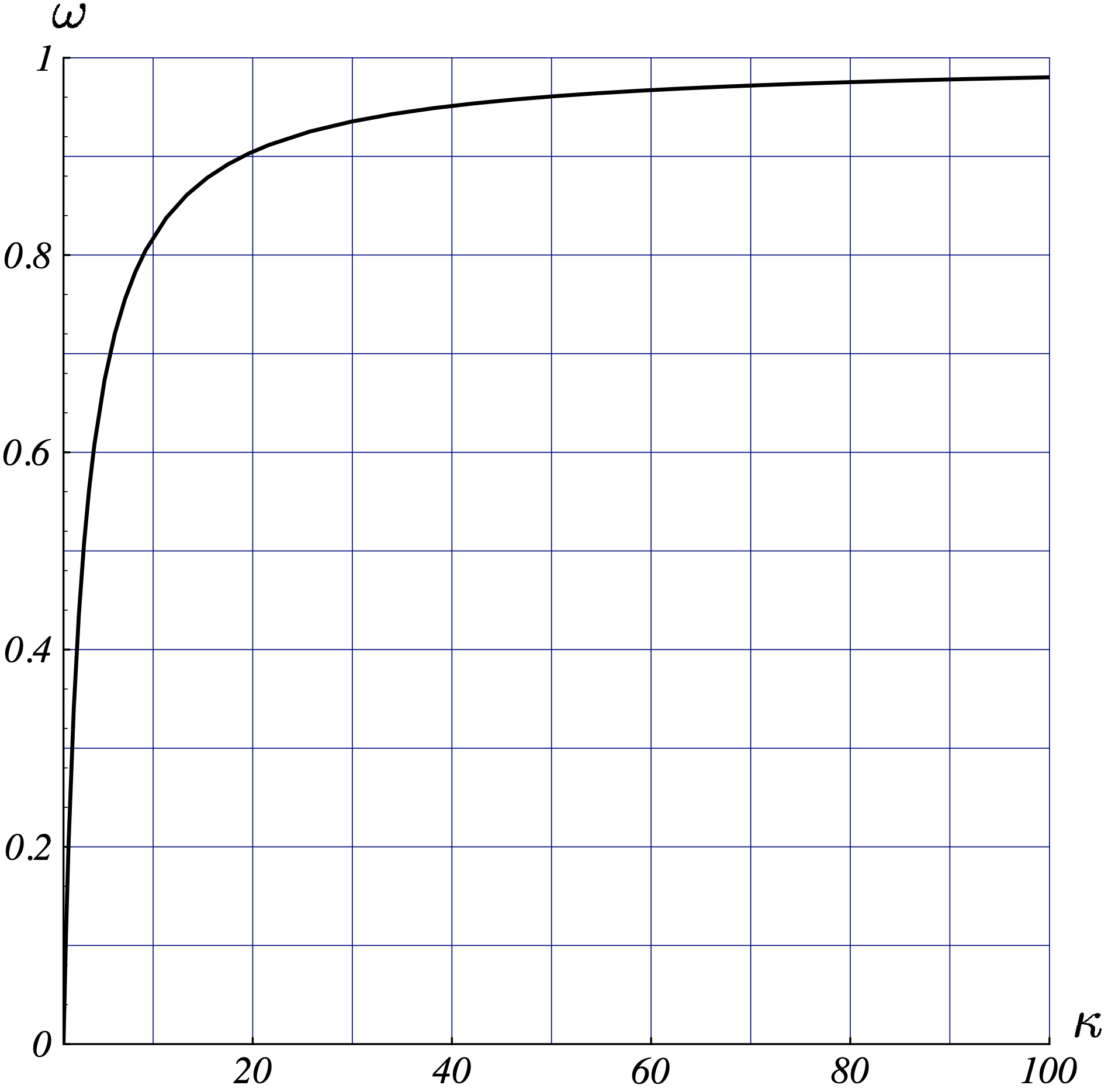
现在我来回答一下前文埋下的一个问题。即，梯度法的收敛速度和 $\omega$ 之间的关系：因为 $$ \begin{aligned} \frac{f(\vec{x}_{(i)}) - f(\vec{x}^\star)}{f(\vec{x}_{(0)}) - f(\vec{x}^\star)} = \frac{\frac{1}{2} \vec{e}_{(i)}^\mathrm{T} \mathbf{A} \vec{e}_{(i)}}{\frac{1}{2} \vec{e}_{(0)}^\mathrm{T} \mathbf{A} \vec{e}_{(0)}} = \frac{\Vert \vec{e}_{(i)} \Vert_{\mathbf{A}}^2}{\Vert \vec{e}_{(0)} \Vert_{\mathbf{A}}^2} = \omega^2, \end{aligned} $$ 所以 $\omega$ 越大，收敛速度就越慢。换句话说，$\Vert \vec{e}_{(i)} \Vert^2_{\mathbf{A}}$ 反应的是第 $i$ 轮迭代时当前解和最优解之间在优化目标上的差距。 结合上式和 $(\textrm{e.q. 17})$ 可得 $$ \Vert \vec{e}_{(i)} \Vert_{\mathbf{A}} \leq \bigg( \frac{\kappa-1}{\kappa+1} \bigg)^i \Vert \vec{e}_{(0)} \Vert_{\mathbf{A}}, $$ 所以 $$ \begin{equation} \frac{f(\vec{x}_{(i)}) - f(\vec{x}^\star)}{f(\vec{x}_{(0)}) - f(\vec{x}^\star)} \leq \bigg( \frac{\kappa - 1}{\kappa + 1} \bigg)^{2i}. \tag{e.q. 18} \end{equation} $$ 这就是当 $\mathbf{A}$ 为对称正定阵时梯度法的最坏收敛速率。

最后

下半部分请移步 理解共轭梯度法（下）· 共轭梯度法 。本文档的 pdf 版本可以在 《理解共轭梯度法》下载。

转载申请

本作品采用 知识共享署名 4.0 国际许可协议 进行许可，转载时请注明原文链接。您必须给出适当的署名，并标明是否对本文作了修改。